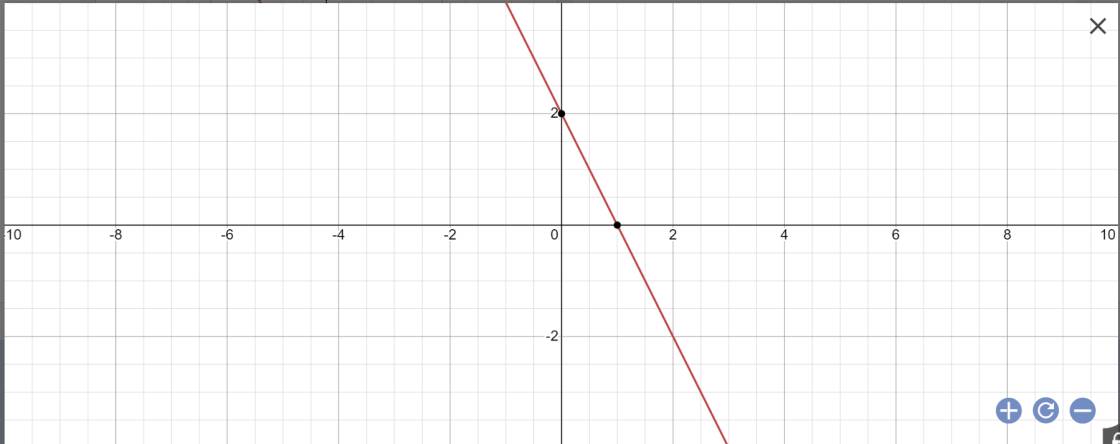
cho h/s y=(m-1)x +2m
a; Vẽ đồ thị h/s với m=-1. Gọi giao điểm của đồ thị vừa vẽ là M và N. tính đt tam giác OMN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 12 2023
a: Thay x=-1 và y=-2 vào y=(m-1)x+2m, ta được:
\(-\left(m-1\right)+2m=-2\)
=>2m-m+1=-2
=>m+1=-2
=>m=-3
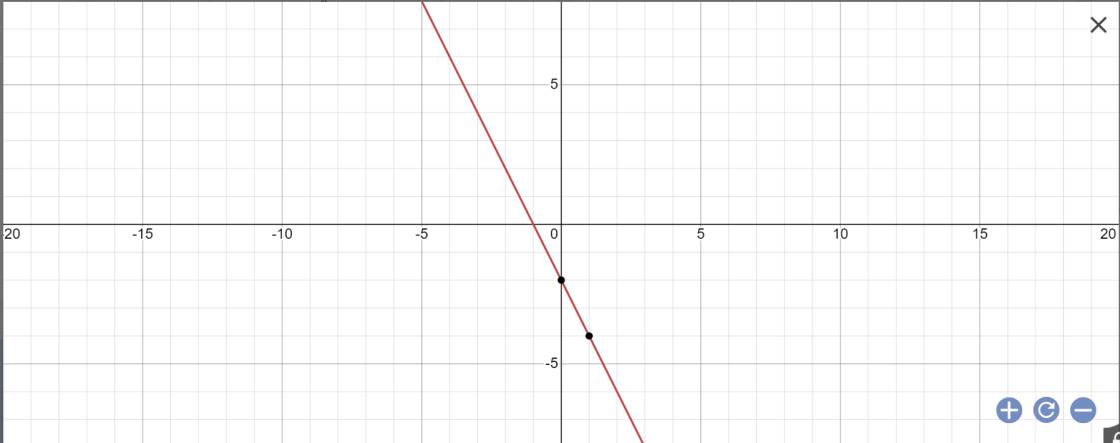
b: Khi m=-1 thì \(y=\left(-1-1\right)x+2\cdot\left(-1\right)=-2x-2\)
CM
16 tháng 6 2018
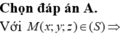
( x + 5 ) 2 + ( y + 5 ) 2 + ( z - 14 ) 2 = 324
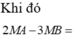
Dấu bằng đạt tại
D
2
2 tháng 3 2022
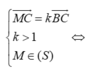
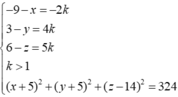
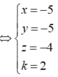
a, (d) đi qua I(1;3)
<=> 3 = 2(m-1) + m^2 + 2m
\(\Leftrightarrow m^2+4m-2=3\Leftrightarrow m^2+4m-5=0\)
\(\Leftrightarrow\left(m-1\right)\left(m+5\right)=0\Leftrightarrow m=1;m=-5\)
2 tháng 3 2022
a: Thay x=1 và y=3 vào (d),ta được:
2(m-1)+m2+2m=3
\(\Leftrightarrow m^2+4m-2-3=0\)
=>(m+5)(m-1)=0
=>m=-5 hoặc m=1
DM
9 tháng 2 2017
+) y = f(x) = \(\frac{1}{2x-2}\)
GTBT được xác định khi \(2x-2\ne0\rightarrow x\ne1\)
Vậy \(x\ne1\) thì hàm số y = f(x) = \(\frac{1}{2x-2}\) xác định.
+) y = f(x) = \(\frac{2x-1}{3x-2}\ne0\)
GTBT được xác định khi \(3x-2\ne0\rightarrow x\ne\frac{2}{3}\)
Vậy \(x\ne\frac{2}{3}\) thì hàm số y = f(x) = \(\frac{2x-1}{3x-2}\) xác định.
AH
Akai Haruma
Giáo viên
4 tháng 4 2018
Lời giải:
Vì \(M\in (d): x+y+1=0\) nên gọi tọa độ của \(M(a,-a-1)\)
Khi đó:
\(\overrightarrow{MA}=(1-a, 2+a+1)=(1-a,a+3)\)
\(\overrightarrow{MB}=(-2-a, a+1)\)
\(\overrightarrow{MC}=(2-a, -1+a+1)=(2-a, a)\)
\(\Rightarrow 2\overrightarrow{MA}-3\overrightarrow{MB}+2\overrightarrow{MC}=2(1-a,a+3)-3(-2-a,a+1)+2(2-a,a)\)
\(=(12-a, a+3)\)
\(\Rightarrow |2\overrightarrow{MA}-3\overrightarrow{MB}+2\overrightarrow{MC}|=\sqrt{(12-a)^2+(a+3)^2}\)
\(=\sqrt{2a^2-18a+153}=\sqrt{2(a-\frac{9}{2})^2+\frac{225}{2}}\)
Từ đây suy ra để \(|2\overrightarrow{MA}-3\overrightarrow{MB}+2\overrightarrow{MC}|\) min, \(a=\frac{9}{2}\)
\(\Rightarrow M=(\frac{9}{2}, \frac{-11}{2})\)
29 tháng 11 2023
Bài 2:
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot5=3\cdot4=12\)
=>AH=12/5=2,4(cm)
c: ΔAHC vuông tại H
=>\(AH^2+HC^2=AC^2\)
=>\(HC^2=4^2-2,4^2=10,24\)
=>HC=3,2(cm)
ΔAHC vuông tại H
=>\(S_{HAC}=\dfrac{1}{2}\cdot HA\cdot HC=\dfrac{1}{2}\cdot3,2\cdot2,4=1,2\cdot3,2=3,84\left(cm^2\right)\)
Bài 1:
a: Để (1) là hàm số bậc nhất thì m-3<>0
=>m<>3
b: Sửa đề: y=-2x+3
Để (1)//y=-2x+3 thì \(\left\{{}\begin{matrix}m-3=-2\\2m< >3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=1\\m< >\dfrac{3}{2}\end{matrix}\right.\)
=>m=1
c: Khi m=1 thì (d): \(y=\left(1-3\right)x+2\cdot1=-2x+2\)
