Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot5=3\cdot4=12\)
=>AH=12/5=2,4(cm)
c: ΔAHC vuông tại H
=>\(AH^2+HC^2=AC^2\)
=>\(HC^2=4^2-2,4^2=10,24\)
=>HC=3,2(cm)
ΔAHC vuông tại H
=>\(S_{HAC}=\dfrac{1}{2}\cdot HA\cdot HC=\dfrac{1}{2}\cdot3,2\cdot2,4=1,2\cdot3,2=3,84\left(cm^2\right)\)
Bài 1:
a: Để (1) là hàm số bậc nhất thì m-3<>0
=>m<>3
b: Sửa đề: y=-2x+3
Để (1)//y=-2x+3 thì \(\left\{{}\begin{matrix}m-3=-2\\2m< >3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=1\\m< >\dfrac{3}{2}\end{matrix}\right.\)
=>m=1
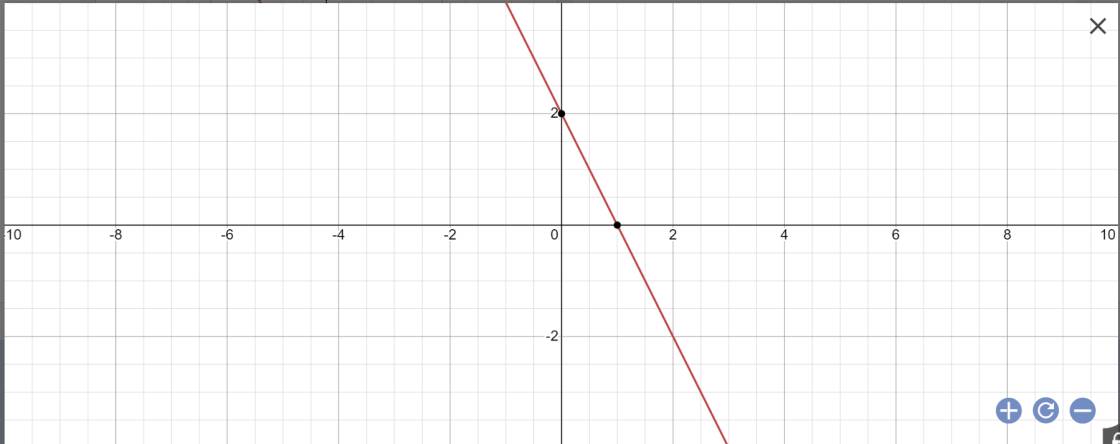
c: Khi m=1 thì (d): \(y=\left(1-3\right)x+2\cdot1=-2x+2\)

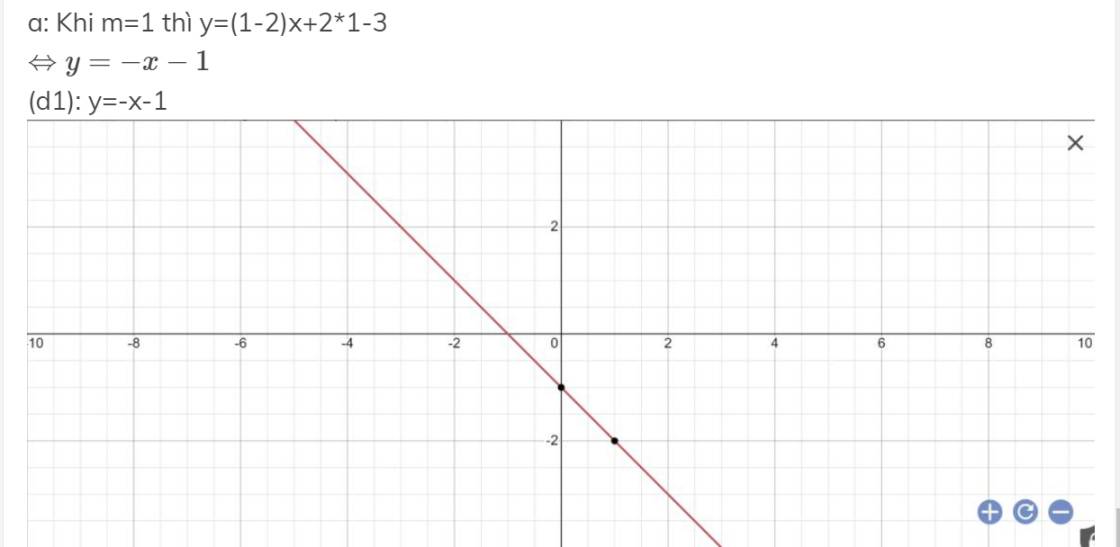
a: Khi m=1 thì y=(1-2)x+2*1-3
\(\Leftrightarrow y=-x-1\)
(d1): y=-x-1
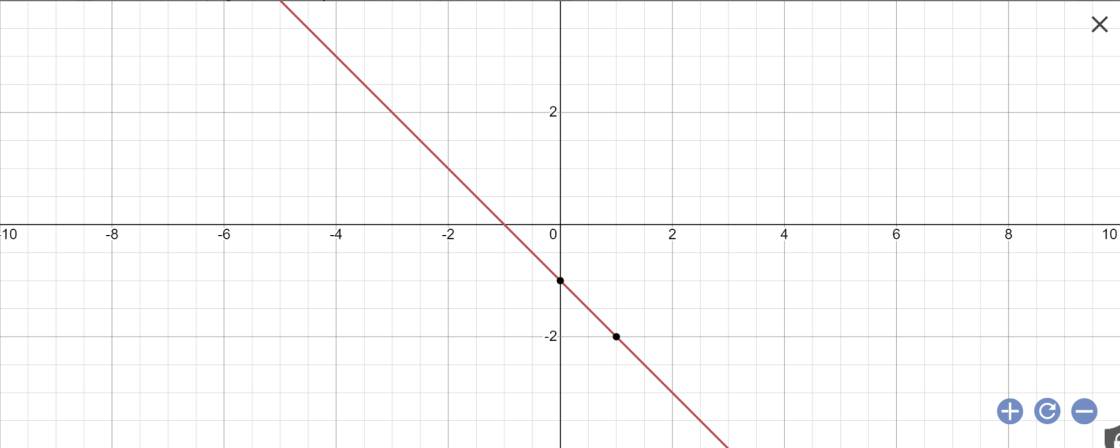
b: Tọa độ A là nghiệm của hệ phương trình sau:
\(\left\{{}\begin{matrix}-x-1=x-5\\y=x-5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2x=-4\\y=x-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2-5=-3\end{matrix}\right.\)
c: \(a_1\cdot a_2=1\cdot\left(-1\right)=-1\)
=>\(\left(d1\right)\perp\left(d2\right)\)

b: Tọa độ Q là:
2x-4=-x+4 và y=2x-4
=>x=8/3 và y=16/3-4=4/3
c: Tọa độ M là:
x=0 và y=2x-4=-4
Tọa độ N là:
x=0và y=-x+4=4
Q(8/3;4/3); M(0;-4); N(0;4)
\(MQ=\sqrt{\left(0-\dfrac{8}{3}\right)^2+\left(-4-\dfrac{4}{3}\right)^2}=\dfrac{8\sqrt{5}}{3}\)
\(QN=\sqrt{\left(0-\dfrac{8}{3}\right)^2+\left(4-\dfrac{4}{3}\right)^2}=\dfrac{8\sqrt{2}}{3}\)
\(MN=\sqrt{\left(0-0\right)^2+\left(4+4\right)^2}=8\)
\(C=\left(\dfrac{8\sqrt{5}}{3}+\dfrac{8\sqrt{2}}{3}+8\right)\left(cm\right)\)
Xét ΔMNQ có
\(cosN=\dfrac{NM^2+NQ^2-QM^2}{2\cdot NM\cdot NQ}=\dfrac{\sqrt{2}}{2}\)
nên góc N=45 độ
\(S=\dfrac{1}{2}\cdot NM\cdot NQ\cdot sinN=\dfrac{1}{2}\cdot\dfrac{8\sqrt{2}}{3}\cdot8\cdot\dfrac{\sqrt{2}}{2}=\dfrac{32}{3}\)
\(cosM=\dfrac{MQ^2+MN^2-QN^2}{2\cdot MQ\cdot MN}\)
nên góc M=27 độ
=>góc Q=180-45-27=108 độ

a: Để đây là hàm số bậc nhất thì m+1<>0
=>m<>-1
b: Để hàm số đồng biến thì m+1>0
=>m>-1
Để hàm số nghịch biến thì m+1<0
=>m<-1
c: Thay x=-1/2 và y=2 vào (d), ta được:
-1/2(m+1)+m=2
=>-1/2m-1/2+m=2
=>1/2m=5/2
=>m=5

a, Thay x = 1 vào (d) : y = 2x <=> y = 2
Vậy (d) đi qua A(1;2)
(P) cắt (d) tại A(1;2) <=> a = 2
c, Hoành độ giao điểm (P) ; (d) tm pt
\(2x^2-2x=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=0\end{matrix}\right.\)
-> Thay x = 0 vào ta được y = 0
Vậy (P) cắt điểm thứ 2 là B(0;0)