Cho\(\Delta\)ABC có M,N là trung điểm AB, AC. CM MN//BC; MN=\(\frac{1}{2}\)BC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài làm
Trên tia đối của tia NM lấy điểm P sao cho MN = NP
Nối M với C
Xét tam giác AMN và tam giác CPN có:
AN = NC ( N là trung điểm của AC )
/ ANM = / PNC ( hai góc đối đỉnh )
MN = NP ( cmt )
=> tam giác AMN = tam giác CPN ( c.g.c )
=> / AMN = / CPN ( hai góc tương ứng )
Mà hai góc đó ở vị trí so le trong
=> AM // CP
Do đó: MB // CP ( Vì M thuộc AB )
=> / BCM = / CMP ( hai góc so le trong )
=> / PCM = / BMC( hai góc so le trong )
Xét tam giác BMC và tam giác PCM có:
/ BMC = / PCM ( cmt )
MC chung
/ BCM = / CMP ( cmt )
=> tam giác BMC = tam giác PCM ( g.c.g )
=> MP = BC
Mà N là trung điểm của MP ( Vì MN = NP )
=> MN = 1/2BC ( 1 )
Lại có: / PMC = / BCM ( cmt )
Mà hai góc này ở vị trí so le trong.
=> MN // BC ( 2 )
Từ ( 1 ) và ( 2 ) => MN // BC và MN = 1/2BC
Vậy MN // BC và MN = 1/2BC ( đpcm )
* Kết luận: Trong một tam giác, đường thẳng nối trung điểm của hai cạnh bất kì luôn song song và bằng một phần hai cạnh còn lại.
# Chúc bạn học tốt #
Bộ bạn chưa đọc 3 cách chứng minh đường trung bình của mình ở đây à:
Câu hỏi của ๖ۣۜK-๖ۣۜA๖L๖ۣۜ♡K♡ 2๖ۣۜK7 (Team TST 9) - Toán lớp 7 - Học toán với OnlineMath
Không được đăng câu hỏi lên diễn đàn vs mục đích hỏi nhé-đó là nội quy.

a) Ta có: BE⊥AO(gt)
CF⊥AO(gt)
Do đó: BE//CF(Định lí 1 từ vuông góc tới song song)
⇒\(\widehat{EBO}=\widehat{FCO}\)(Hai góc so le trong)
Xét ΔEBO vuông tại E và ΔFCO vuông tại F có
BO=CO(O là trung điểm của BC)
\(\widehat{EBO}=\widehat{FCO}\)(cmt)
Do đó: ΔEBO=ΔFCO(cạnh huyền-góc nhọn)
⇒OE=OF(Hai cạnh tương ứng)
b) Xét ΔOBF và ΔOCE có
OB=OC(O là trung điểm của BC)
\(\widehat{BOF}=\widehat{COE}\)(hai góc đối đỉnh)
OF=OE(cmt)
Do đó: ΔOBF=ΔOCE(c-g-c)
⇒\(\widehat{FBO}=\widehat{ECO}\)(hai góc tương ứng)
mà \(\widehat{FBO}\) và \(\widehat{ECO}\) là hai góc ở vị trí so le trong
nên CE//BF(Dấu hiệu nhận biết hai đường thẳng song song)

a: Xét ΔABC có
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
Do đó: MN//BC
b: Xét ΔABD có
MK//BD
nên \(\dfrac{MK}{BD}=\dfrac{AM}{AB}=\dfrac{5}{6}\left(1\right)\)
Xét ΔACD có
KN//DC
nên \(\dfrac{KN}{DC}=\dfrac{AN}{AC}=\dfrac{5}{6}\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(\dfrac{KM}{BD}=\dfrac{KN}{DC}\)
mà BD=DC
nên KM=KN
hay K là trung điểm của MN

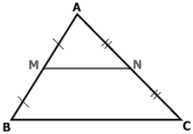
Theo giả thiết ta có M là trung điểm của AB, N là trung điểm của AC
⇒ MN là đường trung bình của Δ ABC.
Áp dụng định lý 2, ta có MN = 1/2BC.
⇒ MN = 1/2BC = 1/2.4 = 2( cm )

a) T/có : AB = AC (gt)
=> Tam giác ABC cân tại A (đn)
AN = NB = AB/2 (N là trung điểm của AB)
AM = MC = AC/2 (M là trung điểm của AC)
mà AB = AC (tam giác ABC cân tại A)
=> AM = MC = AN = NB
Xét tam giác ABM và tam giác ACN có:
AM = AN (cmt)
A là góc chung
AB = AC (tam giác ABC cân tại A)
=> Tam giác ABM = Tam giác ACN (c.g.c)
Xét tam giác BNC và tam giác CMB có:
BN = CN (cmt)
NBC = MCB (tam giác ABC cân tại A)
BC là cạnh chung
=> Tam giác BNC = Tam giác CMB (c.g.c)
b) MB = ME (M là trung điểm của BE)
NC = NF (N là trung điểm của CF)
mà MB = NC (tam giác BNC = tam giác CMB)
=> ME = NF
T/có : ANF = BNC (2 góc đối đỉnh)
AME = CMB (2 góc đối đỉnh)
mà BNC = CMB (tam giác BNC = CMB)
=> ANF = AME
Xét tam giác ANF và tam giác AME có:
AN = AM (cmt)
ANF = AME (cmt)
NF = ME (cmt)
=> Tam giác ANF = tam giác AME (c.g.c)
=> AF = AE (2 cạnh tương ứng)
=> A là trung điểm của FE
c) Vì AM = AN (cmt)
=> Tam giác ANM cân tại A
=> ANM = (180 − NAM) : 2 (1)
Tam giác ABC cân tại A
=> ABC = (180 − BAC) : 2 (2)
Từ (1) và (2) => ANM = ABC
mà 2 góc này ở vị trí đồng vị
=> MN // BC
Xét tam giác ANF và BNC có:
AN = NB (N là trung điểm của AB)
ANF = BNC (2 góc đối đỉnh)
NF = NC (N là trung điểm của FC)
=> Tam giác ANF = Tam giác BNC (c.g.c)
=> FAN = CBN (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong
=> AF // BC
mà MN // BC (cmt)
=> EF // MN // BC (đpcm)

Kẻ đường thẳng MF sao cho N là trung điểm của MF
+) Xét \(\Delta AMN\)và \(\Delta CFN\) có :
\(\hept{\begin{cases}AM=MB\\\widehat{ANM}=\widehat{CNF}\\AN=NC\end{cases}\Rightarrow\Delta AMN=\Delta CFN\left(c.g.c\right)}\)
\(\Rightarrow\widehat{MAN}=\widehat{FCN}\)( 2 góc tương ứng )
FC = AM ( 2 cạnh tương ứng ) ( 1 )
Mà \(\widehat{MAN}\widehat{\text{và}FCN}\) ở vị trí sole trong
=> AM // FC ( dấu hiệu ) (2 )
Mà AM = MB (3)
Từ (1) (2) (3)
=> FC // MB và FC = MB
+) Xét tứ giác MFCB có : FC // MB và FC = MB
=> MFCB là hình bình hành ( dấu hiệu nhận biết )
=> MF // BC ( tính chất)
=> MN // BC .
+) Vì MFCB là hình bình hành
=> MF = BC (4)
Ta có : MN + NF = MF
Mà MN = NF
=> \(MF=\frac{1}{2}MN\left(5\right)\)
Từ ( 4) và(5)
\(\Rightarrow MN=\frac{1}{2}BC\)
các bạn học lớp mấy