Cho tam giác ABC có diện tích 60m2. MN song song với BC ; MA=MB,NA=NC
A) Tính diện tích tam giác AMN
B) Cho đoạn CH=1/3BC . Tính diện tích hình thang BMNH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải
Ta có hình vẽ:
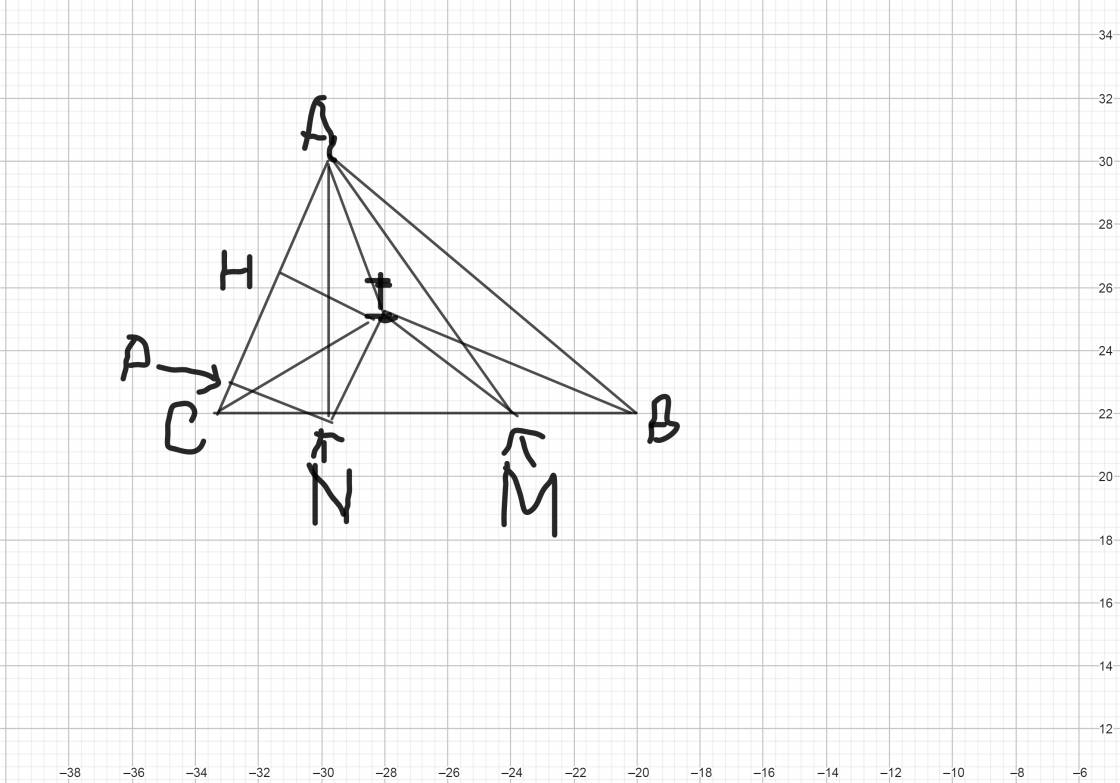
Ta có:
_______________________________
HI=PN(Vì:IM song song AC)
S HTG ACI = AC * HI S HTG ACI= S HTG ANC
2 ______>> Tương tự : S HTG ABI = S HTG AMB
S HTG ANC = AC * PN
2
_________________________________
¼ HTG ABC = S HTG AMB = S HTG ANC
Vì cùng có chiều cao là AN, đáy là ¼ BC nên S HTG ANC = S HTG ABM .
Ta có:
S HTG ANC = S HTG AMB =S HTG ABI = S HTG AMB .
S 1 HTG trong số các hình trên (hay S HTG IAC và IAB) là:
500 : 4 = 125 (cm2)
S HTG IBC là :
500 – (125 * 2) = 250 (cm2)
Đáp số: 125cm2;
250cm2
k giúp mk vs ak
a: MA=MB
=>M là trung điểm của AB
=>\(S_{AMC}=\dfrac{1}{2}\times S_{ABC}=30\left(m^2\right)\)
NA=NC
=>N là trung điểm của AC
=>\(S_{AMN}=\dfrac{1}{2}\times S_{AMC}=15\left(m^2\right)\)
b: \(S_{BNC}=\dfrac{1}{2}\times S_{ABC}=30\left(m^2\right)\)
\(CH=\dfrac{1}{3}CB\)
=>\(S_{NHC}=\dfrac{1}{3}\times S_{NBC}=10\left(m^2\right)\)
Ta có: \(S_{AMN}+S_{NHC}+S_{BMNH}=S_{ABC}\)
=>\(S_{BMNH}+15+10=60\)
=>\(S_{BMNH}=35\left(m^2\right)\)