Cho tứ diện ABCD có AB=2; CD=4 và các cạnh còn lại cùng bằng 6. Tính diện tích mặt cầu ngoại tiếp tứ diện S.ABCD.
A. 1156 π 31
B. 1156 π 93
C. 47 π
D. 1280 π 93
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp
Sử dụng công thức tính nhanh thể tích khối tứ diện biết ba cạnh và ba góc cùng xuất phát từ một đỉnh:
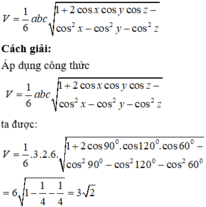

Phương pháp
Sử dụng công thức tính nhanh thể tích khối tứ diện biết ba cạnh và ba góc cùng xuất phát từ một đỉnh:
![]()
Cách giải:
Áp dụng công thức ![]()
ta được: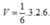
![]()
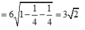
Chọn D.

Bạn xem hình vẽ ở đây nhé: https://i.imgur.com/sh8KysD.png
Gọi CD giao AB tại O, Đặt OD=a, OA=b.
Xét tam giác OAD vuông tại O ta có
a^2 + b^2 =25
Xét tam giác OBC vuông tại O ta có
(a+8^2 )+ (b+2^2=13^2
Từ đó tính được a=84/17 hoặc a=4. Loại a=84/17vì với a=84/17 thì b<0
Với a=4 suy ra b=3. Khi đó SABCD=SOBC-SOAD=24
Bạn xem hình vẽ ở đây nhé: https://i.imgur.com/sh8KysD.png
Gọi CD giao AB tại O, Đặt OD=a, OA=b.
Xét tam giác OAD vuông tại O ta có \(a^2+b^2=25\)
Xét tam giác OBC vuông tại O ta có \(\left(a+8\right)^2+\left(b+2\right)^2=13^2\)
Từ đó tính được a \(=\frac{87}{17}\)hoặc a = 4. Loại a = \(\frac{87}{17}\)vì với a = \(\frac{87}{17}\) thì \(b< 0\)
Với a = 4 suy ra b = 3. Khi đó \(^SABCD=^SOBC-^SOAD=24\)

Đáp án B
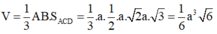
Phương án nhiễu.
A. Sai vì 2 cách: một là thấy số 1 3 cứ chọn, hai là trong công thức thể tích thiếu 1 3 diện tích đáy.
C. Sai vì thiếu 1 3 trong công thức thể tích.

Chọn B.
Phương pháp:
Thể tích của tứ diện có các cạnh đôi một vuông góc và các cạnh đó có độ dài lần lượt là a, b, c là
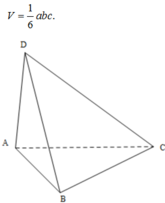
Cách giải:
Tứ diện ABCD có AB, AC, AD đôi một vuông góc
=> Thể tích khối tứ diện ABCD là:
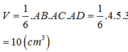
Đán án C
Gọi G là trung điểm của EF thì G chính là tâm mặt cầu ngoại tiếp tứ diện.
Ta có C E 2 = C B 2 + C A 2 2 − A B 2 4 = 6 2 + 6 2 2 − 2 2 4 = 35 ,
E F 2 = C E 2 − C F 2 = 35 − 2 2 = 31
⇒ G F = 31 2 ⇒ R = G C = G F 2 + C F 2 = 31 4 + 4 = 47 2 .
Vậy diện tích mặt cầu cần tính là:
S = 4 π R 2 = 4 π . 47 4 = 47 π .