Cho tam giác ABC vuông tại A có AB= 9 cm; BC - AC = 3 cm. Tính BC, AC.
1 tick cho ai trả lời đúng và nhanh nhất nhé!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 7 2021
Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=15^2-9^2=144\)
hay AC=12(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\\CH=\dfrac{12^2}{15}=\dfrac{144}{15}=9,6\left(cm\right)\end{matrix}\right.\)
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AH^2+HB^2=AB^2\)
\(\Leftrightarrow AH^2=9^2-5.4^2=51,84\)
hay AH=7,2(cm)
12 tháng 3 2022
Theo định lí Pytago tam giác ABC vuông tại A
\(AC=\sqrt{BC^2-AB^2}=12cm\)
Vì BD là pg \(\dfrac{AB}{BC}=\dfrac{AD}{DC}\Rightarrow\dfrac{DC}{BC}=\dfrac{AD}{AB}\)
Theo tc dãy tỉ số bằng nhau ta có
\(\dfrac{DC}{BC}=\dfrac{AD}{AB}=\dfrac{12}{24}=\dfrac{1}{2}\Rightarrow DC=\dfrac{15}{2}cm;DA=\dfrac{9}{2}cm\)
CM
13 tháng 6 2018
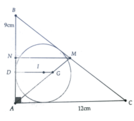
Gọi M là trung điểm của BC
Ta tính được AG = 2 3 AM = 10cm
Gọi N là trung điểm của AB => MN//AC, MN ⊥ AB
D,I,G thẳng hàng
<=> A G A M = A D A N = 2 3 <=> A D 2 A N = 1 3 <=> A D A B = 1 3
Ta có AD = r nội tiếp = A B + A C - B C 2 <=> A B 3 = A B + A C - B C 2
<=> AB+3AC = 3BC = A B 2 + A C 2
<=> 3AC = 4AB (đpcm)
Áp dụng kết quả trên ta có: AD = A B + A C - B C 2 = 3cm
=> ID = DA = 3cm => IG = DG – ID = 1cm
CD
2
8 tháng 8 2019
vì BH=9 , HC=16
=> BC=25
xét tam giác ABC ...., ta có
BC^2=CA^2+AB^2
hay 25^2=20^2 +Ab^2
625=400 + AB^2
AB^2=225
AB=15
xét tam giác ABH...., ta có
AB^2=AH^2 + BH^2
hay 15^2= Ah^2 + 9^2
225= AH^2 +81
AH^2= 144
AH=12
thêm kl và những chỗ còn thiếu vào nhé
CD
4
KN
8 tháng 8 2019
Ta có: \(BC=BH+CH=9+16=25\)
Áp dụng định lý Py- ta - go vào \(\Delta ABC\), ta được:
\(AB^2=BC^2-AC^2\)
\(\Leftrightarrow AB^2=25^2-20^2\)
\(\Leftrightarrow AB^2=625-400\)
\(\Leftrightarrow AB^2=225\)
\(\Leftrightarrow AB=\sqrt{225}=15\)
Áp dụng định lý Py- ta - go vào \(\Delta AHC\), ta được:
\(AH^2=AC^2-CH^2\)
\(\Leftrightarrow AH^2=20^2-16^2\)
\(\Leftrightarrow AH^2=400-256\)
\(\Leftrightarrow AH^2=144\)
\(\Leftrightarrow AH=\sqrt{144}=12\)
8 tháng 8 2019
Bài làm
BC=BH+HC=9+6=25(cm)BC=BH+HC=9+6=25(cm)
Áp dụng định lý Py-ta-go với tam giác ABC vuông tại A, ta có:
BC2=AB2+AC2BC2=AB2+AC2
⇒AB2=BC2+AC2=252−202⇒AB2=BC2+AC2=252−202
=625−400=225=152=625−400=225=152
Vậy AB=15cm
Áp dụng định lý Py-ta-go với tam giác AHC vuông tại H, ta có:
AH2=AC2−HC2=202−162=122AH2=AC2−HC2=202−162=122
Vậy AH= 12cm
# Học tốt #
16 tháng 6 2023
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
=>BH/BA=BA/BC
=>BA^2=BH*BC
b: BC=căn 9^2+12^2=15cm
AH=9*12/15=7,2cm
Theo giả thiết : BC - AC = 3 => AC = BC -3
THeo định lý Pytago : BC2 = AB2 + (BC-3)2
BC2 = AB2 + BC2 - 6BC + 9
0 = AB2 - 6BC + 9 => 6BC = AB2 + 9
6BC = 92 + 9 = 90 => BC = 15 (cm)
Ta có : AC = 15 - 3 = 12 (cm)