Cho tam giác ABC kẻ AH vuông góc với BC ( H thuộc BC ) . Gọi M là trung điểm của BC . Biết AH ; AM chia góc ở đỉnh A của tam giác thành 3 góc = nhau . Tính các góc của tam giác ABC .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đây nha

Lấy X, Y lần lượt đối xứng A qua H và M.
Dễ thấy ΔΔAMB cân( đường cao đồng thời là phân giác)
suy ra ABXM là hình thoi
ta có M vừa là trung điểm BC vừa là trung điểm AY
=> ABYC là hình bình hành
suy ra CY=AB=XM và XMBˆ=ABCˆXMB^=ABC^ = MCYˆMCY^
=> CY∖∖XMCY∖∖XM
=>XYCM là hình bình hành=> MC=XY
mà ta còn có AC=BY ( hbh)
BX=AM ( hình thoi)
=> ΔAMC=ΔBXYΔAMC=ΔBXY
=> XBYˆ=MACˆ=XAYˆXBY^=MAC^=XAY^
mà AY∖∖BXAY∖∖BX
=>AXBY là hình thang cân
=>AB=XY=MC=MB=AM
=> tam giác AMB đều
=>BAMˆ=Bˆ=60oBAM^=B^=60o=>Aˆ=90o,C=30oˆ

ΔAHD vuông tại H
nên AH<AD
Vì góc ADH<90 độ
=>góc ADM>90 độ
=>AD<AM
=>AH<AD<AM
=>AD nằm giữa AH và AM

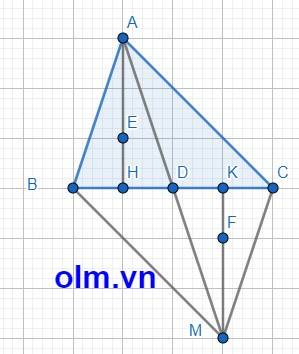
Xét tam giác ACD và tam giác MBD có:
AD = DM (gt)
BD = DC (gt)
\(\widehat{BDM}\) = \(\widehat{ADC}\) (hai góc đối đỉnh)
⇒ \(\Delta\)ACD = \(\Delta\) MBD (c-g-c)
Xét tứ giác ABMC có
AD = DM
BD = DC
⇒ tứ giác ABMC là hình bình hành vì tứ giác có hai đường chéo căt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành.
⇒ AC // BM
⇒ \(\widehat{ABM}\) = \(\widehat{MCA}\) (vì tứ giác ABMC là hình bình hành)
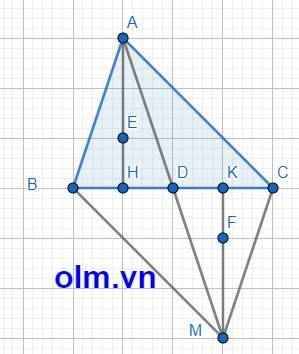
xét tam giác ACD và tam giác MBD có
AD=DM [ gt ]
BD=DC[ gt ]
BDM = ADC hai góc đối đỉnh
suy ra tam giác ACD= tam giác MBD [ c-g-c]
xét tứ giác ABMC có
AD = DM
BD=DC
suy ra tứ giác ABMC là hình bình hành vì tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành
suy ra ABM=MCA vì tứ giác ABMC là hình bình hành .

Bạn vẽ hình ra nhé!
Do tam giác ABD vuông cân tại A => góc DAM + góc BAH = 90º. Trong tam giác vuông ABH có góc ABH + góc BAH = 90º => góc DAM = góc ABH (cùng phụ với một góc bằng nhau)
Xét tam giác vuông ADM và tam giác vuông BAH có:
AD = AB (gt)
góc DAM = góc ABH (cmt)
=> tam giác ADM = tam giác BAH (cạnh huyền - góc nhọn)
=> DM = AH
Cmtt ta có: tam giác ANE = tam giác CHA => EN = AH
=> DM = EN (cùng bằng AH)
Lại có: DM // EN (cùng _|_ AH) mà DM = EN (cmt) => tứ giác DMEN là hình bình hành => MN cắt DE tại trung điểm mỗi đường hay MN đi qua trung điểm của DE.
Chúc bạn học giỏi!
tk nha bạn
thank you bạn
(^_^)
Do tam giác ABD vuông cân tại A => góc DAM + góc BAH = 90º. Trong tam giác vuông ABH có góc ABH + góc BAH = 90º => góc DAM = góc ABH (cùng phụ với một góc bằng nhau)
Xét tam giác vuông ADM và tam giác vuông BAH có:
AD = AB (gt)
góc DAM = góc ABH (cmt)
=> tam giác ADM = tam giác BAH (cạnh huyền - góc nhọn)
=> DM = AH
Cmtt ta có: tam giác ANE = tam giác CHA => EN = AH
=> DM = EN (cùng bằng AH)
Lại có: DM // EN (cùng _|_ AH) mà DM = EN (cmt) => tứ giác DMEN là hình bình hành => MN cắt DE tại trung điểm mỗi đường hay MN đi qua trung điểm của DE.
