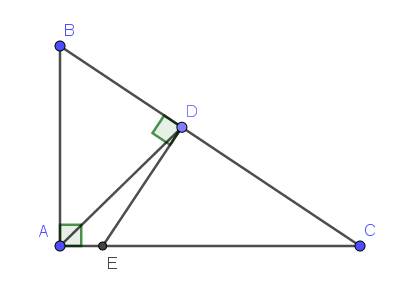
Cho ∆ABC vuông tại A. Đường phân giác của góc ABC cắt AC tại D. a) Cho BC= 25cm; AC= 9 cm. Tính tỉ số DA/DC. b) Qua D kẻ DH vuông góc với BC tại H. Chứng minh ∆ABC ~ ∆HDC từ đó chứng minh CH. CB=CD. CA. c) Gọi E là hình chiếu của A trên BC. Chứng minh BA/BA= HC/HE. d) O là giao điểm của BD và AH. Qua B kẻ đường thẳng song song với AH cắt các tia CO và CA lần lượt tại M và N. Chứng minh M là trung điểm của BN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: DA/DC=BA/BC=căn 25^2-9^2/25=căn 544/25
b: Xét ΔHDC vuông tại H và ΔABC vuông tại A có
góc C chung
=>ΔHDC đồng dạng với ΔABC
=>CH/CA=CD/CB
=>CH*CB=CA*CD

a) Sửa lại đề cho hợp lí nha, phải là AD=DH
Xét tg BAD và BHD có :
BD-chung
\(\widehat{ABD}=\widehat{HBD}\left(gt\right)\)
\(\widehat{BAC}=\widehat{BHD}=90^o\)
=> Tg BAD=BHD(cạnh huyền-góc nhọn)
=> AD=HD (đccm)
b) Xét tg DHC vuông tại H có : HD<CD (cạnh góc vuông luôn nhỏ hơn cạnh huyền)
Mà HD=DA
=>DA<CD
c)Gọi giao điểm của BD và KC là I
Xét tg KBC có :
=> BI là đường cao thứ 3 của tg KBC
- Xét tg BIK và BIC có :
BI-chung
\(\widehat{KBI}=\widehat{CBI}\left(gt\right)\)
\(\widehat{BIK}=\widehat{BIC}=90^o\)(BI là đường cao tg BCK)
=> Tg BIK=BIC (g.c.g)
=> BK=KC
=> Tg BCK cân tại B (đccm)
#H

Lời giải:
a. Xét tam giác $DEC$ và $ABC$ có:
$\widehat{C}$ chung
$\widehat{EDC}=\widehat{BAC}=90^0$
$\Rightarrow \triangle DEC\sim \triangle ABC$ (g.g)
b.
Từ tam giác đồng dạng phần a suy ra $\frac{DE}{DC}=\frac{AB}{AC}(1)$
Vì $AD$ là phân giác của góc $\widehat{A}$ nên:
$\frac{BD}{DC}=\frac{AB}{AC}(2)$
Từ $(1); (2)\Rightarrow \frac{DE}{DC}=\frac{BD}{DC}$
$\Rightarrow DE=BD$ (đpcm)

Tam giác ABC vuông tại A ﴾gt﴿
=> góc BAD + DAC = 90\(^0\)﴾1﴿
Tam giác HAD vuông tại H có:
góc HDA + HAD = 90\(^0\) ﴾2﴿
Mà góc HAD = góc DAC ﴾ vì AD là p/g của HAC ﴿ ﴾3﴿
Từ ﴾1﴿ ﴾2﴿ và ﴾3﴿ => góc BAD = góc BDA => tam giác ABD cân tại B
=> AB=BD﴾ t/c tam giác cân ﴿
Tam giác ABC có AH là đường cao :
AB 2 = BH * BC ﴾ Hệ thức lượng﴿
<=> AB 2 = ﴾ BD‐6﴿ * BC
<=> AB 2 = ﴾AB‐6﴿ * 25
<=> AB 2 ‐25AB + 150 = 0
<=> ﴾ AB‐10﴿ * ﴾AB‐15﴿=0
<=> AB=10 hoặc AB=15

a: AC=căn 10^2-6^2=8
b: Xét ΔCHD vuông tại H và ΔCAB vuông tại A có
góc C chung
=>ΔCHD đồng dạng với ΔCAB
=>CH/CA=CD/CB
=>CH*CB=CD*CA
c: BK=BA^2/BC=3,6cm
AK=6*8/10=4,8cm
Xét ΔBAK có BI là phân giác
nên IK/BK=AI/AB
=>IK/3=AI/5=(AI+IK)/(3+5)=4,8/8=0,6
=>IK=1,8cm

a) Ta có: ΔDEC vuông tại D(ED\(\perp\)BC tại D)
nên \(\widehat{DEC}+\widehat{C}=90^0\)(Hai góc nhọn phụ nhau)(1)
Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{ABC}+\widehat{C}=90^0\)(Hai góc nhọn phụ nhau)(2)
Từ (1) và (2) suy ra \(\widehat{DEC}=\widehat{ABC}\)
a: DA/DC=BA/BC=\(\dfrac{\sqrt{25^2-9^2}}{25}=\dfrac{4\sqrt{34}}{25}\)
b: Xet ΔABC vuông tại A và ΔHDC vuông tạiH có
góc C chung
=>ΔABC đồng dạg với ΔHDC
=>CA/CH=CB/CD
=>CA*CD=CH*CB