Số nghiệm thuộc đoạn 0 ; 5 π 2 của phương trình 2 sin x − 1 = 0 là
A. 2
B. 3
C. 1
D. 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
PT
1
CM
7 tháng 9 2018
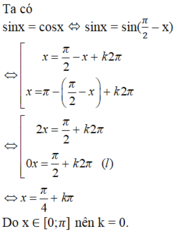
Vậy chỉ có 1 nghiệm của phương trình thuộc [0; .
Đáp án là A.
PT
1
CM
22 tháng 4 2017
Ta có sin x = cos x ⇔ sin x = sin π 2 − x
⇔ x = π 2 − x + k 2 π x = π − π 2 − x + k 2 π
⇔ x = π 4 + k π , k ∈ ℤ
Do x ∈ 0 ; π nên k = 0
Vậy phương trình chỉ có một nghiệm duy nhất
ĐÁP ÁN A
CM
8 tháng 9 2018
Đáp án D
P T ⇔ cos x + 1 ≠ 0 sin 2 x = 0 ⇔ cos x ≠ − 1 2 x = k π ⇔ x ≠ π + k 2 π x = k π 2 ⇒ x = k 2 π x = π 2 + k π k ∈ ℤ .
x ∈ 2 π ; 4 π ⇒ 2 π ≤ k 2 π ≤ 4 π 2 π ≤ π 2 + k π ≤ 4 π ⇔ 1 ≤ k ≤ 2 3 2 ≤ k ≤ 7 2
Suy ra PT có 4 nghiệm thuộc đoạn 2 π ; 4 π .
CM
3 tháng 6 2018
Đáp án D
P T ⇔ m + 1 1 − c os 2 x 2 − sin 2 x + cos 2 x = 0 ⇔ sin 2 x + m − 1 2 c os 2 x = m + 1 2 .
PT có nghiệm ⇔ 1 2 + m − 1 2 2 ≥ m + 1 2 2 ⇔ m ≤ 1.
Vì m ∈ − 2018 ; 2018 ⇒ có 2020 giá trị nguyên của m.
Đáp án B
Ta có 2 sin x − 1 = 0 ⇔ sin x = 1 2 ⇔ x = π 6 + k 2 π x = 5 π 6 + k 2 π k ∈ ℤ
Mặt khác 0 ≤ x ≤ 5 π 2 suy ra x = π 6 ; 13 π 6 ; 5 π 6 . Vậy phương trình có 3 nghiệm