Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Lời giải:
$y'=\frac{2x}{\sqrt{2x^2+1}}$
$y'>0\Leftrightarrow 2x>0\Leftrightarrow x>0$ hay $x\in (0;+\infty)$
$y'< 0\Leftrightarrow 2x< 0\Leftrightarrow x\in (-\infty;0)$
Vậy hàm số đồng biến trên $(0;+\infty)$ và nghịch biến trên $(-\infty; 0)$
Đáp án A.
a) Tập xác định \(D = \mathbb{R}\backslash \left\{ 0 \right\}\).
Lấy \({x_1},{x_2} \in \left( {0; + \infty } \right)\) sao cho \({x_1} < {x_2}\).
Xét \(f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \frac{1}{{{x_1}}} - \frac{1}{{{x_2}}} = \frac{{{x_2} - {x_1}}}{{{x_1}{x_2}}}\)
Do \({x_1} < {x_2}\) nên \({x_2} - {x_1} > 0\)
\({x_1},{x_2} \in \left( {0; + \infty } \right) \Rightarrow {x_1}{x_2} > 0\)
\( \Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) > 0 \Leftrightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
Vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\).
b) Lấy \({x_1},{x_2} \in \left( { - \infty ;0} \right)\) sao cho \({x_1} < {x_2}\).
Xét \(f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \frac{1}{{{x_1}}} - \frac{1}{{{x_2}}} = \frac{{{x_2} - {x_1}}}{{{x_1}{x_2}}}\)
Do \({x_1} < {x_2}\) nên \({x_2} - {x_1} > 0\)
\({x_1},{x_2} \in \left( { - \infty ;0} \right) \Rightarrow {x_1}{x_2} > 0\)(Cùng dấu âm nên tích cũng âm)
\( \Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) > 0 \Leftrightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
Vậy hàm số nghịch biến trên \(\left( { - \infty ;0} \right)\).
TXĐ: D = [0; 2]
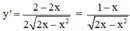
+ Hàm số đồng biến
⇔ y’ > 0
⇔ 0 < x < 1.
+ Hàm số nghịch biến
⇔ y’ < 0
⇔ 1 < x < 2.
Vậy hàm số đồng biến trên khoảng (0; 1), nghịch biến trên khoảng (1; 2).
Đáp án là C
Câu III sai vì thiếu dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I
Câu IV sai vì có thể vô số điểm trên I xuất hiện rời rạc thì vẫn có thể nghịch biến trên khoảng I
Đáp án là C
I.Sai ví dụ hàm số y = x 3 đồng biến trên
(−¥; +¥) nhưng y' ³ 0, "x Î (−¥; +¥)
II.Đúng
III.Đúng
Đáp án: C.
Gợi ý: Loại A, D vì tập xác định của hàm số là 25 - x 2 ≥ 0 ⇔ -5 ≤ x ≤ 5.
Loại B, vì
x |
-5 |
0 |
y |
0 |
5 |
1.
\(y'=2cosx-2sin2x=2cosx-4sinx.cosx=2cosx\left(1-2sinx\right)\)
\(y'=0\Rightarrow\left[{}\begin{matrix}cosx=0\\sinx=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}\\x=\dfrac{\pi}{6}\\x=\dfrac{5\pi}{6}\end{matrix}\right.\)
Hàm đồng biến trên các khoảng \(\left(0;\dfrac{\pi}{6}\right)\) và \(\left(\dfrac{\pi}{2};\dfrac{5\pi}{6}\right)\)
2.
Xét hàm \(f\left(x\right)=x^2-2x-3\)
\(f\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
\(f'\left(x\right)=2x-2=0\Rightarrow x=1\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;3\right)\)
nghịch biến trên khoảng:
Chọn đáp án A. Có