Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = π cosx , x ∈ ℝ A. M = π

PT

Pham Trong Bach

17 tháng 6 2017

Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = π cosx , x ∈ ℝ A. M = π ; m = 1 π B. M = π ; m = 1 C. M = π ; m = 1 D. M = π ; m = 1 π ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

17 tháng 6 2017

Đúng(0)

PT

Pham Trong Bach

23 tháng 5 2019

Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f(x) = sinx (1+cosx) trên đoạn 0 ; π A. M = 3 3 2 ; m = 1 B. M = 3 3 4 ; m = 0 C. M = 3 3 ; m = 1 D. M = 3 ; m = 1 ...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

23 tháng 5 2019

Đúng(0)

PT

Pham Trong Bach

11 tháng 7 2017

Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f x = sin x 1 + cos x trên đoạn 0 ; π A. M = 3 3 2 ; m = 1 B. M = 3 3 4 ; m = 0 C. M = 3 3 ; m = 1 D. M = 3 ; m = 1 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

11 tháng 7 2017

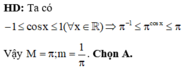
Đáp án B

Cách 1: Tư duy tự luận

Xét hàm số f x = sin x 1 + cos x trên 0 ; π

Đạo hàm f ' x = cos x 1 + cos x − sin 2 x = 2 cos 2 x + cos x − 1 ;

f ' x ⇔ cos x = − 1 cos x = 1 2 ⇔ x = π + k 2 π x = ± π 3 + k 2 π k ∈ ℤ

Do x ∈ 0 ; π nên x = π 3 ; x = π .

Ta có

f 0 = f π = 0 ; f π 6 = 3 3 4

Vậy

M = max 0 ; π f x = 3 3 4 ; m = min 0 ; π f x = 0

Cách 2: Sử dụng máy tính cầm tay

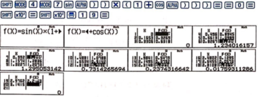
Quan sát bảng giá trị, ta thấy

M = max 0 ; π f x ≈ 1,295... ≈ 3 3 4 ; m = min 0 ; π f x = 0

Đúng(0)

PT

Pham Trong Bach

20 tháng 11 2017

Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = - 1 + 2 cos x 2 - 3 sin x + c o s x trên ℝ . Biểu thức M + N + 2 có giá trị bằng:

A. 0

B. 4 2 - 3

C. 2

D. 2 + 3 + 2

#Mẫu giáo

1

CM

Cao Minh Tâm

20 tháng 11 2017

Đáp án C

Ta có y = - 1 + 2 - 3 . 2 sin x c o s x + 2 cos 2 x = 2 - 3 . sin 2 x + cos 2 x .

Áp dụng bất đẳng thức Bunhicopxki, có

2 - 3 . sin 2 x + cos 2 x 2 ≤ 2 - 3 2 + 1 2 . sin 2 2 x + cos 2 2 x = 8 - 4 3

Suy ra y 2 ≤ 8 - 4 3 ⇔ 8 - 4 3 ≤ y ≤ 8 - 4 3 . Vậy M + N + 2 = 2.

Đúng(0)

PT

Pham Trong Bach

16 tháng 4 2017

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 sin x + cos 2x trên đoạn 0 , π . Khi đó 2M + m bằng

A. 4

B. 5/2

C. 7/2

D. 5

#Toán lớp 11

1

CM

Cao Minh Tâm

16 tháng 4 2017

Đúng(0)

PT

Pham Trong Bach

4 tháng 11 2017

Gọi M m , theo thứ tự là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = sinx+cos2x+sin3xtrên đoạn 0 ; π . Tính P = M+m A. B. C. ...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

4 tháng 11 2017

Chọn B

Đúng(0)

PT

Pham Trong Bach

25 tháng 11 2017

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 sin x + c os 2 x trên đoạn 0 ; π . Khi đó 2 M + m bằng A. 4 B. 5 2 C. 7 2 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

25 tháng 11 2017

Đáp án A

Ta có: y = 2 s i nx+cos 2 x

= 2 sin x + 1 − 2 sin 2 x → t → s inx y = f x = − 2 t 2 + 2 t + 1.

Với x ∈ 0 ; π ⇒ t ∈ 0 ; 1 .

Xét hàm số f t = − 2 t 2 + 2 t + 1 trên 0 ; 1 có f ' t = − 4 t + 2.

Ta có: f ' t = 0 ⇔ t = 1 2 .

Tính f 0 = 1 ; f 1 2 = 3 2 ; f 1 = 1.

Vậy M = 3 2 m = 1 ⇒ 2 M + m = 4.

Đúng(0)

PT

Pham Trong Bach

21 tháng 7 2017

Gọi M , m theo thứ tự là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = s inx+ cos 2 x + sin 3 x trên đoạn 0 ; π . Tính P = M + m A. P = 16 27 B. P = − 19 + 13 13 27 C. P = − 19 − 13 13 27 D. P = − 16 27 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

21 tháng 7 2017

Đáp án B

Đúng(0)

L

loveyoongi03

1 tháng 9 2021

Cho hàm số y=\(\dfrac{sin^2x}{cosx\left(sinx-cosx\right)}+\dfrac{1}{4}\) với x thuộc \(\left(\dfrac{\text{π}}{4};\dfrac{\text{π}}{2}\right)\). Tìm giá trị nhỏ nhất của hàm số

#Toán lớp 11

1