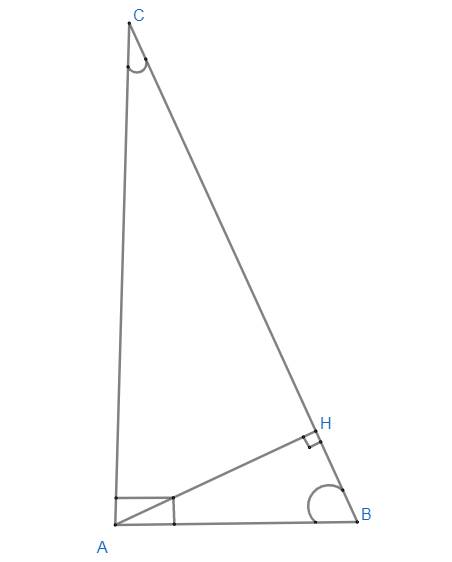
Trong ΔABC,ΔABC, kẻ AH⊥BC(H∈BC) sao cho \(\widehat{BAH}\)= \(2\widehat{CAH}\). Tính \(\widehat{B}\); \(\widehat{C}\) biết \(\widehat{A}=72^O\). (VẼ CẢ HÌNH)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 11 2017
Theo đề ta có: \(\widehat{BAH}=2\widehat{CAH}\Rightarrow\widehat{A}=3\widehat{CAH}\)
Mà \(\widehat{A}=72^o\left(gt\right)\) \(\Rightarrow3\widehat{CAH}=72^o\)
\(\Rightarrow\widehat{CAH}=24\) \(\Rightarrow BAH=24^o.2=48^o\)
Ta lại có: \(\widehat{B}+\widehat{BAH}=90^o\) (định lí của một tam giác vuông)
hay \(\widehat{B}+48^o=90^o\Rightarrow\widehat{B}=42^o\)
Tương tự: \(\widehat{C}+\widehat{CAH}=90^o\)
hay \(\widehat{C}+24^o=90^o\Rightarrow\widehat{C}=66^o\)
Vậy góc B có số đo là \(42^o\)
góc C có số đo là \(66^o\)
1 tháng 5 2021
Vì ΔABC vuông tại A
==> BC2 = AC2 +AB2 ( Định lý Pitago )
BC2 = 42 + 32
BC2 = 27
==> BC = √27
1 tháng 5 2021
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
Vậy: BC=5cm
H
22 tháng 12 2023
a)
Xét 2 tam giác vuông ABC và HAC có:
\(\widehat{C}\) chung
=> tg ABC \(\sim\) td HAC (g.g)
=> \(\widehat{ABC}=\widehat{HAC}\)
b)
Xét 2 tg vuông ACB và HAB có:
\(\widehat{B}\) chung
=> tg ACB \(\sim\) tg HAB (g.g)
=> \(\widehat{ACB}=\widehat{HAB}\)
25 tháng 8 2016
a) Xét hai tam giác vuông ABH và ACH
có:+AB=AC( \(\Delta ABC\) cân tại A)
+AH: cạnh chung
Vậy \(\Delta ABH=\Delta ACH\left(ch-cgv\right)\)
=> HB=HC( hai cạnh tương ứng)
b) Vì \(\Delta ABH=\Delta ACH\left(cmt\right)\)
nên: góc BAH=góc CAH( hai góc tương ứng)
^..^ 
^_^
25 tháng 8 2016
a) Xét \(\Delta\nu ABH\) và \(\Delta\nu ACH\) có :
\(AB=AC\left(gt\right)\)
\(AH\) là cạnh chung
Do đó : \(\Delta\nu ABH=\Delta\nu ACH\left(ch-gn\right)\)
\(\Rightarrow HB=HC\) ( vì hai cạnh tương ứng )
b ) Vì : \(\Delta\nu ABH=\Delta\nu ACH\)
\(\Rightarrow\widehat{BAH}=\widehat{CAH}\)
20 tháng 4 2017
a) Hai tam giác vuông ABH và ACH có:
AB=AC(gt)
AH cạnh chung.
Nên ∆ABH=∆ACH(Cạnh huyền-cạnh góc vuông)
Suy ra HB=HC
b)∆ABH=∆ACH(Câu a)
Suy ra ^BAH=^CAH(Hai góc tương ứng)
20 tháng 4 2017
a) Hai tam giác vuông ABH và ACH có:
AB=AC(gt)
AH cạnh chung.
Nên ∆ABH=∆ACH(Cạnh huyền-cạnh góc vuông)
Suy ra HB=HC
b)∆ABH=∆ACH(Câu a)
Suy ra ˆBAHBAH^=ˆCAHCAH^(Hai góc tương ứng)
Xem thêm tại: http://loigiaihay.com/bai-63-trang-136-sach-giao-khoa-toan-7-tap-1-c42a5157.html#ixzz4envied4H
a) Hai tam giác vuông ABH và ACH có:
AB=AC(gt)
AH cạnh chung.
Nên ∆ABH=∆ACH(Cạnh huyền-cạnh góc vuông)
Suy ra HB=HC
b)∆ABH=∆ACH(Câu a)
Suy ra ˆBAH^=ˆCAH(Hai góc tương ứng)
26 tháng 5 2017
a) Xét tam giác AHB và tam giác AHC có:
\(\widehat{AHB}=\widehat{AHC}=90^o\)
AB=AC(tam giác ABC cân)
\(\widehat{ABC}=\widehat{ACB}\)(tam giác ABC cân)
Do đó tam giác AHB=tam giác AHC(ch-gn)
Suy ra HB=HC(hai cạnh tương ứng)
b)Vì tam giác AHB=tám giác AHC(câu a)
Nên \(\widehat{BAH}=\widehat{CAH}\)(hai góc tương ứng)
14 tháng 3 2020
a, Xét \(\Delta ABC\),ta có:
\(\widehat{A}=90\)
=> \(\widehat{B}+\widehat{C}=90\) (1)
Xét \(\Delta CAH\),ta có:
\(\widehat{AHC}=90\)
=>\(\widehat{CAH}+\widehat{C}=90\) (2)
Từ (1) và (2)=>\(\widehat{B}=\widehat{CAH}\) (đpcm)
b, Xét \(\Delta BAH\),ta có:
\(\widehat{AHB}=90\)
=>\(\widehat{B}+\widehat{BAH}=90\) (3)
Từ (1) và (3)=>\(\widehat{C}=\widehat{BAH}\) (đpcm)
14 tháng 3 2020
a, tam giác AHB vuông tại H (gt) => ^B + ^HAB = 90 (đl)
^BAC = 90 (gt) => ^HAB + ^CAH = 90
=> ^B = ^CAH
b, tương tự a
19 tháng 3 2021
Sửa tam giác ABC cân tại A nhé chứ là tam giác vuông thì chỉ có c.g thôi
a, Xét tam giác BHA và tam giác AHC ta có :
AH _ chung
^BHA = ^AHC = 900
^ABH = ^ACH ( gt ) vì ABC cân tại A
Vậy tam giác BHA = tam giác AHC ( g.c.g )
=> BH = HC ( 2 cạnh tương ứng )
b, Xét tam giác BAH và tam giác CAH ta có :
BH = HC ( cmt )
^AHB = ^AHC = 900
AH _ chung
Vậy tam giác BAH = tam giác CAH ( c.g.c )
=> ^BAH = ^CAH ( 2 góc tương ứng )
19 tháng 3 2021
a) Xét tam giác ABH và tam giác ACH vuông tại H có:
+) AB = AC (chứng minh trên)
+) Góc B = góc C (cmt)
=> Tam giác ABH = tam giác ACH (cạnh huyền - góc nhọn)
=> HB = HC (2 cạnh tương ứng)
b) Vì tam giác ABH = tam giác ACH nên:
=> Góc BAH = góc CAH (2 góc tương ứng)
18 tháng 5 2017
Chứng minh:
a, Xét \(\Delta ABH\) và \(\Delta ACH\), có:
\(\)AB=AC (tam giác ABC cân tại A) -> cạnh huyền
AH: cạnh chung -> cạnh góc vuông
\(\widehat{AHB}=\widehat{AHC}->gócvuông\)
=> \(\Delta ABH=\Delta ACH\left(cạnhhuyền-cạnhgócvuông\right)\)
=> \(HB=HC\) (2 cạnh tương ứng)
b, Vì \(\Delta ABH=\Delta ACH\left(cạnhhuyền-cạnhgócvuông\right)\left(cmt\right)\)
=> \(\widehat{BAH}=\widehat{CAH}\) (2 góc tương ứng)
CHÚC BẠN HỌC TỐT!
18 tháng 5 2017
Hình tự vẽ nhé
a, Xét tam giác ABH và tam giác ACH có :
AB=AC
Cạnh AH chung
góc AHB = góc AHC
=> tam giác ABH = tam giác ACH ( cạnh huyền góc nhọn )
Suy ra : HB=HC
b, Ta có : tam giác ABH = tam giác ACH ( câu a )
=> Góc BAH = Góc CAH (2 cạnh tương ứng )
Chúc bạn học tốt 