Cho ΔABC có \(\widehat{ABC}=50^0\); \(\widehat{BAC}=70^0\). Phân giác trong góc ACB cắt AB tại M. Trên MC lấy điểm N sao cho \(\widehat{MBN}=40^0\). Chứng mỉnh rằng BN = MC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, tam giác ABC cân tại A (gt)
=> góc B = (180 - góc A) : 2
góc A = 50 (gt)
=> góc B = (180 - 50) : 2
=> góc B = 65
b, xét tam giác AMB và tam giác AMC có : AB = AC do tam giác ABC cân tại A (gt)
góc ABC = góc ACB do tam giác ABC cân tại A (gT)
BM = MC do M là trđ của BC (gt)
=> tam giác AMB = tam giác AMC (c-g-c)
=> góc AMB = góc AMC (đn)
mà góc AMB + góc AMC = 180 (kb)
=> góc AMB = 90
=> AM _|_ BC (đn)
b, tam giác AMB = tam giác AMC (Câu b)
=> góc MAB = góc MAC (đn) mà AM nằm giữa AB và AC
=> AM là pg của góc BAC (đn)
A)VÌ \(\Delta ABC\)CÂN TẠI A
\(\Rightarrow\hept{\begin{cases}AB=AC\\\widehat{B}=\widehat{C}\end{cases}}\)
XÉT TAM GIÁC ABC
CÓ\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\left(đ/l\right)\)
THAY\(50^o+\widehat{B}+\widehat{C}=180^o\)
\(\widehat{B}+\widehat{C}=130^o\)
vì\(\widehat{B}=\widehat{C}\)
THAY \(\widehat{C}+\widehat{C}=130^o\)
\(2\widehat{C}=130^o\)
\(\widehat{C}=130^o:2=65^o\)
\(\Rightarrow\widehat{B}=\widehat{C}=65^o\)
B)XÉT\(\Delta BAM\)VÀ\(\Delta CAM\)CÓ
\(BA=CA\left(GT\right)\)
\(\widehat{B}=\widehat{C}\left(GT\right)\)
\(BM=CM\left(GT\right)\)
\(\Rightarrow\Delta BAM=\Delta CAM\left(C-G-C\right)\)
\(\Rightarrow\widehat{M_1}=\widehat{M_2}\)HAI GÓC TƯƠNG ỨNG
MÀ \(\widehat{M_1}+\widehat{M_2}=180^o\left(KB\right)\)
THAY\(\widehat{M_2}+\widehat{M_2}=180^o\)
\(2\widehat{M_2}=180^o\)
\(\widehat{M_2}=180^o:2=90^o\)
VẬY \(AM\perp BC\left(đpcm\right)\)
c) \(AM\perp BC\left(cmt\right)\)
=> AM LÀ ĐƯƠNG CAO CỦA TAM GIÁC ABC
TRONG TAM GIÁC CÂN ĐƯỜNG CAO CŨNG CHÍNH LÀ ĐƯỜNG PHÁP TUYẾN,PHÂN GIÁC,TRUNG TUYẾN
=> AM LÀ PHÂN GIÁC CỦA\(\widehat{BAC}\)

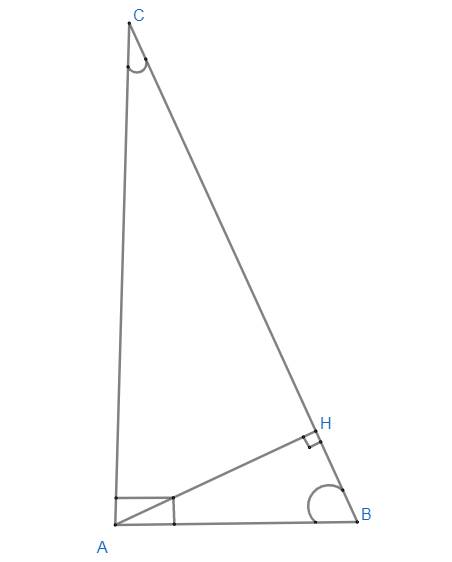
a)
Xét 2 tam giác vuông ABC và HAC có:
\(\widehat{C}\) chung
=> tg ABC \(\sim\) td HAC (g.g)
=> \(\widehat{ABC}=\widehat{HAC}\)
b)
Xét 2 tg vuông ACB và HAB có:
\(\widehat{B}\) chung
=> tg ACB \(\sim\) tg HAB (g.g)
=> \(\widehat{ACB}=\widehat{HAB}\)