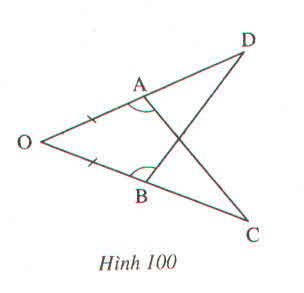
Trên hình 100 ta có \(OA=OB;\widehat{OAC}=\widehat{OBD}\)
Chứng minh rằng AC = BD ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
24 tháng 5 2017
Xét ΔOAC và ΔOBD có:
Nên ΔOAC = ΔOBD (g.c.g)
Suy ra AC = BD (hai cạnh tương ứng).
11 tháng 11 2016
Sao thấy bạn nói "trên hình 90" mà hổng thấy hình đâu?
CM
27 tháng 10 2018
Chọn A.
Gọi khoảng cách từ điểm M đến các mặt bên (OAB), (OBC), (OCA) lần lượt là a, b, c.
Khi đó
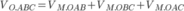
Hay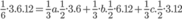 
Thể tích khối gỗ hình hộp chữ nhật theo đề bài là V = abc
Ta có :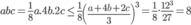
(Theo bất đẳng thức Cô-sin).
Vậy V = abc đạt giá trị lớn nhất bằng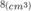 
khi
CM
15 tháng 2 2019
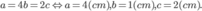
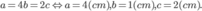
Chọn A.
Gọi khoảng cách từ điểm M đến các mặt bên (OAB), (OBC), (OCA) lần lượt là a, b, c.
Khi đó 
Hay 
Thể tích khối gỗ hình hộp chữ nhật theo đề bài là V = abc
Ta có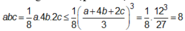 
(Theo bất đẳng thức Cô-sin).
Vậy V = abc đạt giá trị lớn nhất bằng 8( c m 3 ) khi a = 4b = 2c
CM
18 tháng 12 2019
Chọn đáp án A
Gọi a, b, c lần lượt là khoảng cách từ điểm M đến các mặt phẳng (OAB),(OBC) và (OCA) (a,b,c > 0).
Ta có V O . A B C = V M . O A B + V M . O B C + V M . O C A
Thể tích của khối gỗ là
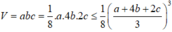
= 1 8 . 12 3 3 = 8 c m 3
Dấu “=” xảy ra khi và chỉ khi khi a =4b =2c =4
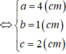
ngu