Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Vậy \(S=4\pi r^2=4\pi\left(\dfrac{a\sqrt{2}}{2}\right)^2=2\pi a^2\) và \(V=\dfrac{4}{3}\pi r^3=\dfrac{4}{3}\pi\left(\dfrac{a\sqrt{2}}{2}\right)^3=\dfrac{1}{3}\pi a^3\sqrt{2}\)
Gọi H là hình chiếu vuông góc của A' trên mặt phẳng (ABCD)
Kẻ HN vuông góc với AB tại N, HM vuông góc với AD tại M
Ta cần tìm chiều cao h=A'H của hình hộp
Dễ dàng chứng minh \(\widehat{A'NH}=60^0\) và \(\widehat{A'MH}=45^0\)
Xét tam giác vuông NHA' và MHB' có
\(NH=\frac{HA'}{tan\widehat{HNA'}}=\frac{h}{\sqrt{3}}\) và \(MH=\frac{HA'}{tan\widehat{HMA'}}=h\)
Xét hình vuông AMHN có \(AH=\sqrt{HN^2+HM^2}=\frac{2h}{\sqrt{3}}\)
Xét tam giác vuông AHA' có \(AH^2+A'H^2=A'A^2\Leftrightarrow h^2+\frac{4}{3}h^2=1\Leftrightarrow h=\sqrt{\frac{3}{7}}\)
Vậy thể tích hình hộp là: \(V=h.\sqrt{3}.\sqrt{7}=\sqrt{\frac{3}{7}}.\sqrt{3}\sqrt{7}=3\)
mình không hiểu rằng bạn muốn tìm thể tích hình lăng trụ nào?có phải là thể tích hình hộp ko?
đầu bài nó chỉ cho như thế thôi, bạn thử tính xem là đáp án nào
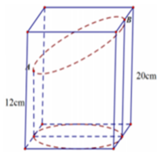
Chọn A.
Gọi khoảng cách từ điểm M đến các mặt bên (OAB), (OBC), (OCA) lần lượt là a, b, c.
Khi đó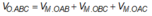
Hay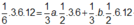
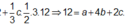
Thể tích khối gỗ hình hộp chữ nhật theo đề bài là V = abc
Ta có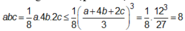
(Theo bất đẳng thức Cô-sin).
Vậy V = abc đạt giá trị lớn nhất bằng 8( c m 3 ) khi a = 4b = 2c