\(2x+5\sqrt{x}=3\)
Tìm \(x\) ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Giống nhau:
+ Các tế bào mầm (noãn nguyên bào, tinh nguyên bào) đều thực hiện nguyên phân liên tiếp nhiều lần
+ Noãn bào bậc 1 và tinh bào bậc 1 đều thực hiện giảm phân để cho giao tử
- Khác nhau:
| Phát sinh giao tử cái | Phát sinh giao tử đực |
| - Noãn bào bậc 1 qua giảm phân I cho thể cực thứ nhất có kích thước nhỏ và noãn bào bậc 2 có kích thước lớn | - Tinh bào bậc 1 qua giảm phân I cho hai tinh bào bậc 2 |
| - Noãn bào bậc 2 qua giảm phân II cho một thể cực thứ hai có kích thước bé và một tế bào trứng có kích thước lớn | - Mỗi tinh bào bậc 2 qua giảm phân II cho hai tinh tử, các tinh tử phát triển thành tinh trùng |
| - Từ mỗi noãn bào bậc 1 qua giảm phân cho hai thể cực và một tế bào trứng, trong đó chỉ có trứng trực tiếp thụ tinh | - Từ mỗi tinh bào bậc 1 qua giảm phân cho bốn tinh trùng, các tinh trùng này đều tham gia vào thụ tinh |

Những dòng thơ trên gợi cho em những suy nghĩ rằng:
- Một hình ảnh người mẹ ham công tiếc việc luôn muốn được chăm chỉ làm việc để lo cho con nhiều thứ tốt hơn. Khi mẹ không còn việc gì làm thì mẹ cảm thấy mình không có hạnh phúc như thường ngày, lo lắng không được lo cho đứa con của mình chu toàn.
- Cảm xúc của một người con hiếu thảo hiểu cho suy nghĩ, tấm lòng, tình yêu thương của người mẹ mà có cảm giác "chợt lo sợ".
- Đồng thời, câu thơ diễn đạt rất tinh tế từ "trổ bông" có sự liên kết cao với từ "cuối mùa", "hết vụ" làm cho lời thơ thêm nhịp điệu và ý thơ diễn đạt sâu sắc, hay hơn.

Hiệu quả: tăng tính liên kết về hình ảnh của câu thơ qua hình ảnh hạt thóc vàng bé nhỏ và cánh đồng, từ đó gợi cảm xúc của tác giả với người mẹ của mình, cảm nhận được sự yêu thương chăm sóc và quan tâm từ mẹ. Đồng thời, câu thơ thêm sinh động và giàu cảm xúc hơn.

\(\sqrt{x^2-x+2}=x\left(1\right)\)
Ta thấy : \(x^2-x+2>0\) nên không cần ĐKXĐ.
\(\left(1\right)\Leftrightarrow x^2-x+2=x^2\left(ĐK:x\ge0\right)\)
\(\Leftrightarrow x^2-x+2-x^2=0\)
\(\Leftrightarrow-x+2=0\)
\(\Leftrightarrow-x=-2\)
\(\Leftrightarrow x=2\left(tm\right)\)
Vậy pt có tập nghiệm : \(S=\left\{2\right\}\)

Bài 1
\(a,\)
- Thời điểm tập trung trên mặt phẳng xích đạo là kì giữa nguyên phân. \(\rightarrow\) \(2n\)\((NST\) \(kép)\)
- Thời điểm NST đơn của các tế bào đang có phân li về 2 cực là kì sau nguyên phân. \(\rightarrow\) \(4n (NST\) \(đơn)\)
- Gọi số tế bào ở kì giữa và kì sau lần lượt là: \(a\) và \(b\) tế bào.
- Theo bài ta có hệ: \(\left\{{}\begin{matrix}78a-156b=-1200\\78a+156b=2640\end{matrix}\right.\rightarrow\left\{{}\begin{matrix}a=9\\b=12\end{matrix}\right.\)
- Mình không rõ là đề bài có lỗi không? Nhưng $a$ và $b$ tính ra là số rất lẻ nên mình làm tròn.
\(b,\) Số tế bào con sau khi kết thúc nguyên phân lần lượt là: $9.2=18(tb)$ và $12.2=24(tb)$
\(c,\) Số NST môi trường cung cấp trong nguyên phân: \(2n.(2-1)=78(NST)\)
Bài 2
Số tâm động ở kì sau của nguyên phân: $4n=16$
Số cromati ở kì giữa của nguyên phân: $4n=16$
Số cromatit ở kì sau của nguyên phân: $0$
Số NST ở kì sau của nguyên phân: $4n=16(NST$ $đơn)$

Sửa đề : \(\dfrac{a^2}{a^2+b}+\dfrac{b^2}{b^2+a}\le1\\ \) (*)
\(< =>\dfrac{a^2\left(b^2+a\right)+b^2\left(a^2+b\right)}{\left(a^2+b\right)\left(b^2+a\right)}\le1\\ < =>a^2b^2+a^3+b^2a^2+b^3\le\left(a^2+b\right)\left(b^2+a\right)\) ( Nhân cả 2 vế cho `(a^{2}+b)(b^{2}+a)>0` )
\(< =>a^3+b^3+2a^2b^2\le a^2b^2+b^3+a^3+ab\\ < =>a^2b^2\le ab\\ < =>ab\le1\) ( Chia 2 vế cho `ab>0` )
Do a,b >0
Nên áp dụng BDT Cô Si :
\(2\ge a+b\ge2\sqrt{ab}< =>\sqrt{ab}\le1\\ < =>ab\le1\)
Do đó (*) luôn đúng
Vậy ta chứng minh đc bài toán
Dấu "=" xảy ra khi : \(a=b>0,a+b=2< =>a=b=1\)
a Sửa đề : Chứng minh \(\dfrac{a^2}{a^2+b}\)+\(\dfrac{b^2}{b^2+a}\)\(\le\) 1 ( Đề thi vào 10 Hà Nội).
Bất đẳng thức trên tương đương :
\(\dfrac{a^2+b-b}{a^2+b}\)+\(\dfrac{b^2+a-a}{b^2+a}\)\(\le\)1
\(\Leftrightarrow\) 1 - \(\dfrac{b}{a^2+b}\)+ 1 - \(\dfrac{a}{b^2+a}\)\(\le\)1
\(\Leftrightarrow\)1 - \(\dfrac{b}{a^2+b}\) - \(\dfrac{a}{b^2+a}\)\(\le\)0
\(\Leftrightarrow\)- \(\dfrac{b}{a^2+b}\)- \(\dfrac{a}{b^2+a}\)\(\le\)-1
\(\Leftrightarrow\)\(\dfrac{a}{b^2+a}\)+ \(\dfrac{b}{a^2+b}\)\(\ge\)1
Xét VT = \(\dfrac{a^2}{ab^2+a^2}\)+ \(\dfrac{b^2}{a^2b+b^2}\)\(\ge\)\(\dfrac{\left(a+b\right)^2}{ab^2+a^2+a^2b+b^2}\) (Cauchy - Schwarz)
= \(\dfrac{\left(a+b\right)^2}{ab\left(b+a\right)+a^2+b^2}\)
\(\ge\)\(\dfrac{\left(a+b\right)^2}{2ab+a^2+b^2}\)
= \(\dfrac{\left(a+b\right)^2}{\left(a+b\right)^2}\)= 1
Vậy BĐT được chứng minh
Dấu '=' xảy ra \(\Leftrightarrow\)a = b = 1

đkxđ: \(\left\{{}\begin{matrix}x\ne0\\y\ne0\end{matrix}\right.\)
pt đầu \(\Leftrightarrow x+\dfrac{2}{x}+y+\dfrac{1}{y}=6\) (3)
pt thứ 2 \(\Leftrightarrow x^2+\dfrac{4}{x^2}+y^2+\dfrac{1}{y^2}=14\) \(\Leftrightarrow\left(x^2+2.x.\dfrac{2}{x}+\dfrac{4}{x^2}\right)+\left(y^2+2y.\dfrac{1}{y}+\dfrac{1}{y^2}\right)=20\)
\(\Leftrightarrow\left(x+\dfrac{2}{x}\right)^2+\left(y+\dfrac{1}{y}\right)^2=20\) (4)
Đặt \(\left\{{}\begin{matrix}x+\dfrac{2}{x}=u\left(\left|u\right|\ge2\sqrt{2}\right)\\y+\dfrac{1}{y}=v\left(\left|v\right|\ge2\right)\end{matrix}\right.\) thì từ (3) và (4) suy ra \(\left\{{}\begin{matrix}u+v=6\\u^2+v^2=20\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}v=6-u\\u^2+\left(6-u\right)^2=20\end{matrix}\right.\)
\(u^2+\left(6-u\right)^2=20\) \(\Leftrightarrow u^2+36-12u+u^2=20\) \(\Leftrightarrow2u^2-12u+16=0\) \(\Leftrightarrow u^2-6u+8=0\) \(\Leftrightarrow\left(u-2\right)\left(u-4\right)=0\) \(\Leftrightarrow\left[{}\begin{matrix}u=2\left(loại\right)\\u=4\left(nhận\right)\end{matrix}\right.\).
\(\Rightarrow v=6-u=2\), suy ra \(\left\{{}\begin{matrix}x+\dfrac{2}{x}=4\\y+\dfrac{1}{y}=2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=2\pm\sqrt{2}\\y=1\end{matrix}\right.\) (nhận).
Vậy hpt đã cho có các nghiệm \(\left(x;y\right)\in\left\{\left(2-\sqrt{2};1\right);\left(2+\sqrt{2};1\right)\right\}\)

\(A=\dfrac{\cos^217^o+2\cos^273^o}{\cot65^o\cot25^o}-\sin^217^o\)
\(A=\dfrac{\left(\cos^217^o+\cos^273^o\right)+\cos^273^o}{\tan25^o\cot25^o}-\sin^217^o\)
(áp dụng công thức \(\cot\alpha=\tan\left(90^o-\alpha\right)\))
\(A=\left(\cos^217^o+\sin^217^o\right)+\sin^217^o-\sin^217^o\)
(áp dụng công thức \(\tan\alpha.\cot\alpha=1\) và \(\cos\alpha=\sin\left(90^o-\alpha\right)\))
\(A=1\)
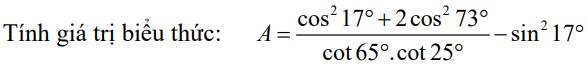
2\(x\) + 5\(\sqrt{x}\) = 3 ( Đkxđ \(x\) ≥ 0)
2\(x\) + 5\(\sqrt{x}\) = 3
⇒2\(x\) + 5\(\sqrt{x}\) - 3 = 0
Đặt \(\sqrt{x}\) = y ( y > 0)
Ta có: 2\(x\) + 5\(\sqrt{x}\) - 3 = 0
⇔2y2 + 5y - 3 = 0
△ = 25 + 24 = 49 > 0
y1 = ( -5 + \(\sqrt{49}\)) : 4 = \(\dfrac{1}{2}\)
y2 = (-5 - \(\sqrt{49}\)): 4 = - 3 (loại)
\(\Rightarrow\) \(\sqrt{x}\) = \(\dfrac{1}{2}\) ⇒ \(x\) = \(\dfrac{1}{4}\)
Vậy \(x\) = \(\dfrac{1}{4}\)