TT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
28 tháng 2 2017
Khảo sát hàm số y = 1 2 x 4 - 3 x 2 + 3 2
- TXĐ: D = R
- Sự biến thiên:
+ Chiều biến thiên:
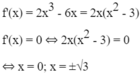
+ Giới hạn tại vô cực:
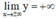
+ Bảng biến thiên:
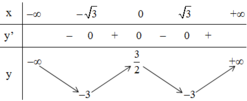
Hàm số đạt cực đại tại x = 0, yCĐ = 3 2
Hàm số đạt cực tiểu tại x =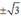 
; yCT = -3.
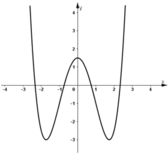
- Đồ thị:
+ Đồ thị hàm số nhận trục tung là trục đối xứng.
+ Đồ thị cắt trục tung tại (0; 1,5).
PT
1
CM
7 tháng 3 2018
+ Bảng biến thiên:
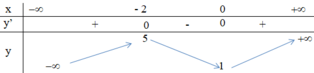
Kết luận:
Hàm số đồng biến trên các khoảng (-∞; -2) và (0; +∞).
Hàm số nghịch biến trên khoảng (-2; 0).
Hàm số đạt cực tiểu tại x = 0 ; y C T = 1 .
Hàm số đạt cực đại tại x = -2 ; y C Đ = 5 .
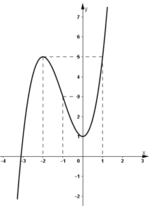
- Đồ thị:
+ Giao với Oy: (0; 1).
+ Đồ thị (C) đi qua điểm (–3; 1), (1; 5).
CM
8 tháng 12 2017
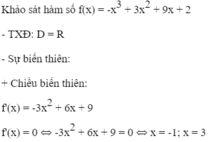
+ Giới hạn:
+ Bảng biến thiên:
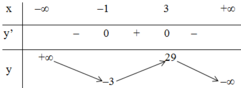
Kết luận:
Hàm số đồng biến trên (-1; 3)
Hàm số nghịch biến trên (-∞; -1) và (3; +∞).
Hàm số đạt cực đại tại x = 3, yCĐ = 29.
Hàm số đạt cực tiểu tại x = -1; y C T = - 3
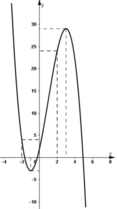
- Đồ thị:
+ Giao với trục tung tại (0; 2).
+ Đi qua các điểm (-2; 4); (2; 24).
MM
0
PT
1
CM
5 tháng 11 2018
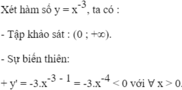
Do đó, hàm số đã cho nghịch biến trên tập xác định.
+ Giới hạn:
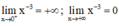
⇒ x = 0 (trục Oy) là tiệm cận đứng của đồ thị hàm số
y = 0 (trục Ox) là tiệm cận ngang của đồ thị hàm số.
+ Bảng biến thiên:
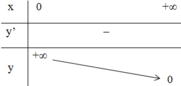
- Đồ thị:
HB
27 tháng 4 2017
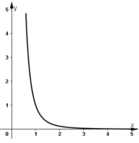
a) Hàm số y=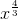 
Tập xác định: (0; +∞).
Sự biến thiên: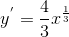 
> 0, ∀x ∈ (0; +∞) nên hàm số luôn luôn đồng biến.
Giới hạn đặc biệt: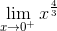 
= 0, 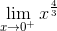= +∞, đồ thị hàm số có tiệm cận.
Bảng biến thiên
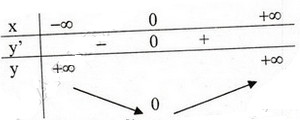
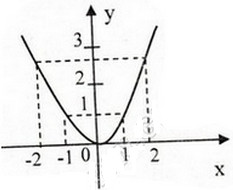
Đồ thị( hình bên). Đồ thị hàm số qua (1;1), (2;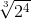
).
b) y=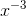 
.
Tập xác định: ℝ \{0}.
Sự biến thiên: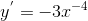 
< 0, ∀xj# 0, hàm nghich biến trong hai khoảng (-∞;0) và (0; +∞).
Giới hạn đặc biệt: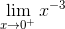
= +∞, 
= -∞, 
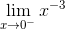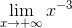= 0,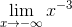 
= 0; đồ thị hàm số nhận trục tung làm tiệm cận đứng, trục hoành làm tiệm cận ngang.
Bảng biến thiên
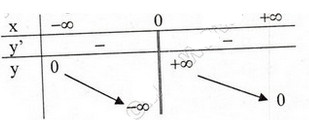
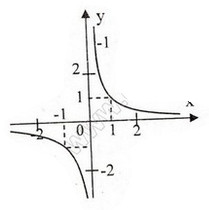
Đồ thị ( hình dưới). Đồ thị qua (-1;-1), (1;1), (2; 
), ( -2;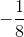 
). Hàm số đồ thị đã cho là hàm số lẻ nên đối xứng qua gốc tọ độ.
PT
1
CM
22 tháng 3 2017
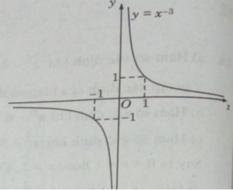
Tập xác định: R\{0}
Hàm số đã cho là hàm số lẻ.
Ta có: y′ < 0, ∀ x ∈ R \ {0} nên hàm số luôn nghịch biến trên các khoảng xác định.
Đồ thị có tiệm cận ngang là trục hoành, tiệm cận đứng là trục tung.
Bảng biến thiên:
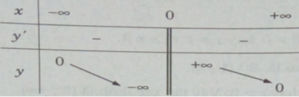
Đồ thị của hàm số có tâm đối xứng là gốc tọa độ.
SG
1
1 tháng 4 2017
a) Tìm tập xác định của hàm số. Xét tính chẵn, lẻ, tuần hoàn của hàm số để thu hẹp phạm vi khảo sát.
b) Sự biến thiên :
+ Xét sự biến thiên của hàm số :
- Tìm đạo hàm bậc nhất y' ;
- Tìm các điểm tại đó y' bằng 0 hoặc không xác định ;
- Xét dấu y' và suy ra chiều biến thiên của hàm số .
+ Tìm cực trị .
+ Tìm các giới hạn tại vô cực, các giới hạn vô cực và tìm các tiệm cận (nếu có).
+ Lập bảng biến thiên tổng kết các bước trên để hình dung ra dáng điệu của đồ thị .
c) vẽ đồ thị (thể hiện các cực trị, tiệm cận, giao của đồ thị với các trục, . . .).
CM
4 tháng 2 2019
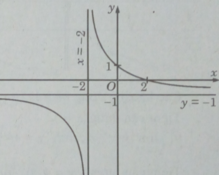
y = - x + 2 x + 2
+) Tập xác định: D = R\{-2}
+) Ta có: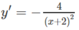 
Bảng biến thiên:
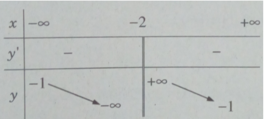
Hàm số nghịch biến trên các khoảng (− ∞ ; −2), (−2; + ∞ )
+) Tiệm cận đứng x = -2 vì
Tiệm cận ngang y = -1 vì
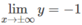
Giao với các trục tọa độ: (0; 1); (2; 0)
Đồ thị
PT
1
CM
6 tháng 12 2017
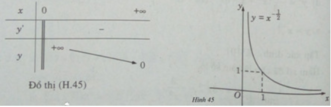
Tập xác định: D = (0; + ∞ )
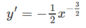
Vì y' < 0 ∀ x ∈ D nên hàm số nghịch biến.
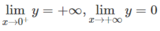
Đồ thị có tiệm cận đứng là trục tung, tiệm cận ngang là trục hoành.
Bảng biến thiên:
Để khảo sát sự biến thiên của hàm số \(y = x^3 - 3x^2 + 4\), ta thực hiện:
1. Tính đạo hàm: Tính đạo hàm \(y'\):
\[ y' = 3x^2 - 6x = 3x(x - 2)\]
2. Tìm nghiệm của đạo hàm: Giải phương trình \(y' = 0\):
\(( 3x(x - 2) = 0 ))
3. Phân tích biến thiên:
- Chọn các khoảng (-∞, 0), (0, 2), (2, +∞) và xét dấu của \(y'\):
- Trên \((-∞, 0)\): \(y' > 0\) và \((2, +∞)\): \(y' > 0\) → hàm tăng.
- trên \(0,2) → hàm giảm
4. Tìm cực trị:
- \(y(0) = 4) và \(y(2) = 2).
- Tại \(x = 0), hàm đạt cực đại; tại \(x = 2), hàm đạt cực tiểu.
5. Vẽ đồ thị:
- Đồ thị cắt trục tung tại y = 4 và có các đặc trưng định hình với cực trị tại \( (0, 4) \) và \( (2, 2) \).
Kết luận: Đồ thị của hàm số có dạng hình chữ M với chiều tăng giảm theo đã phân tích.