Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là C

Ta có:
![]()
theo giao tuyến SD.
Trong (SAD) kẻ AH ⊥ DS
![]()
![]()
![]()
Ta có
![]()
Theo bài

Vì tứ diện SABD có ba cạnh AS, AB, AD đôi một vuông góc nên



Do đó tam giác SAD vuông cân tại A có:
![]()


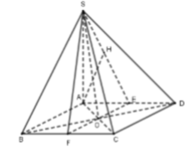
Phương pháp:
- Dựng mặt phẳng chứa SO và song song với AB .
- Sử dụng lý thuyết: Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách từ đường thẳng này đến mặt phẳng song song với nó và chứa đường thẳng kia.
- Đưa bài toán về tính khoảng cách từ điểm đến mặt phẳng và kết luận.
Cách giải:
Gọi E, F lần lượt là trung điểm của AD, BC thì AB / / EF => AB / / (SEF)
Mà ![]()
![]()
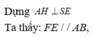
![]()
![]()
![]()
![]()
ABCD là hình vuông cạnh a nên BD = a 2
Dễ dàng chứng minh được ![]()
Tam giác SBD cân có
S
B
D
=
60
0
![]()
Tam giác SAD vuông tại A có ![]()
Tam giác SAE vuông tại A có
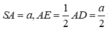
![]()
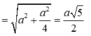
Do đó 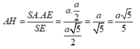
Chọn D.

kẻ CH_|_AD. AD=AH+HD= BC+căn ( CD^2- CH^2). Thay số.
V=1/3. SA. S abcd
Sabcd=1/2.( BC+ AD).AB
d( D; ( SBC))=d( A;(SBC))=AK
kẻ AK _|_ SB

Một đường thẳng muốn vuông góc với một mặt phẳng thì phải vuông góc với 2 đường thẳng chéo nhau chứ bạn? ở ba câu trên bạn mới chứng minh nó vuông với 1 đường mà
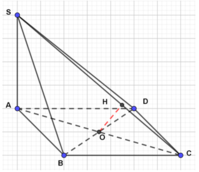
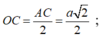
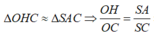
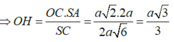
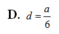

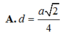
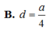
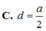
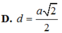






ABCD là hình vuông nên OA=OC => d( A,(SBD) ) = d( C,(SBD) )
Kẻ AH vuông SO
BD vuông AO, BD vuông SA nên BD vuông (SAO) => BD vuông AH
=> AH vuông (SBD)
=> d( A,(SBD) ) = AH
Xét SAO : \(\dfrac{1}{AH^2}\) = \(\dfrac{1}{SA^2}\) + \(\dfrac{1}{AO^2}\)
SA = 3a, AO = \(a\sqrt{2}\) => AH = \(\dfrac{3a\sqrt{22}}{11}\)
Vậy khoảng cách từ C đến (SBD) = \(\dfrac{3a\sqrt{22}}{11}\)