Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sai từ bước 3 bởi vì
f ' 0 - = lim x → 0 - f x - f 0 x - 0 = lim x → 0 - - x - 0 x - 0 = 1
Do f ' 0 + ≠ f ' 0 - nên f '(0) không tồn tại
Đáp án C

giải
Khoảng cách của chúng là
4-2=2
Số thứ 2000 là
2000x2=4000
Đ/S:4000
- Theo trên từ 2 đến 998 có : 1 x 4 + 2 x 45 + 3 x 450 = 1444 ( chữ số )
- Do đó còn : 2000 - 1444 = 556 ( chữ số của các số chẵn có 4 chữ số )
- Số số chẵn có 4 chữ số là : 556 : 4 = 139 ( số )
- Số chẵn có 4 chữ số đầu tiên là 1000, Số chẵn có 4 chữ số thứ 139 là :
1000 + 138 x 2 = 1276
Vậy dãy số chẵn từ 2 đến 1276 gồm đúng 2000 chữ số. Chữ số thứ 2000 của dãy là chữ số 6 ( trong số 1276 )

Đáp án C
Xét dãy số u n = n + 2 . Ta có: u n + 1 = n + 1 + 2 - n + 2 = 1 không đổi ⇒ u n = n + 2 là 1 CSC với công sai d = 1.

Bạn ấn vào từ fx ở ô tạo câu hỏi và chọn biểu tượng ô vuông phân số


Đáp án C
Chọn đáp án C vì dãy ở đây là một CSN có công bội q = 3 2 > 1 , nên dãy 3 2 , 9 4 , 27 8 , . . . , 3 2 n không phải là dãy lùi vô hạn

Đáp án A
Phương pháp:
- Định nghĩa dãy số giảm: Dãy u n được gọi là dãy số giảm nếu u n + 1 < u n n ∈ ℕ * .
- Có thể giải bài toán bằng cách xét các hàm số ở từng đáp án trên tập ℕ * (Dãy số cũng là một hàm số).
- Hàm số nào nghịch biến trên ℕ * thì dãy số đó là dãy số giảm.
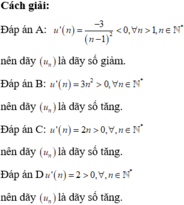

Đáp án A
Phương pháp:1
- Dãy số u n được gọi là bị chặn nếu nó vừa bị chặn trên, vừa bị chặn dưới, nghĩa là: tồn tại số m, M sao cho m ≤ u n ≤ M , ∀ n ∈ ℕ *
Chú ý: Nếu lim u n = ± ∞ thì ta kết luận ngay dãy không bị chặn.
Cách giải:
Đáp án A: 0 < u n = 2 n + 1 n + 1 = 2 n + 1 − 1 n + 1 = 2 − 1 n + 1 < 2 , ∀ n ∈ ℕ * nên u n là dãy bị chặn.
Đáp án B, C, D: lim u n = + ∞ nên các dãy số này đều không là dãy bị chặn.
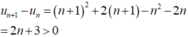
Yêu cầu bạn để đúng lớp!
Yêu cầu bạn để lớp và môn học rõ ràng ạ!