Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

-từ S hình vuông => cạnh tam giác =4
- BK= \(R=\frac{1}{2}.\frac{4}{\cos30}=\frac{4}{\sqrt{3}}\left(cm\right)\)

- Chọn D.
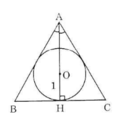
- Gọi O là tâm đường tròn nội tiếp Δ ABC, H là tiếp điểm thuộc BC.
Đường phân giác AO của góc A cũng là đường cao nên A, O, H thẳng hàng.
Ta có: HB = BC, ∠HAC = 30o, AH = 3.OH = 3 (cm)
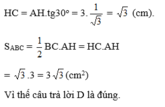

NA/BA = NC/BC
Vì Tam giác ABC vuông tại A, biết AB=3cm,BC=5cm => AC= 4(cm)
=> NC-NA=4 (cm)
=> NC/BC = NA/BA = ( NC-NA)/(BC-AB) = 2
=> NA= BA*2 =6 (cm)

- Chọn D.
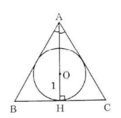
- Gọi O là tâm đường tròn nội tiếp Δ ABC, H là tiếp điểm thuộc BC.
Đường phân giác AO của góc A cũng là đường cao nên A, O, H thẳng hàng.
Ta có: HB = BC, ∠HAC = 30o, AH = 3.OH = 3 (cm)
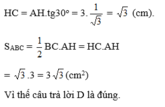

Ta thấy bán kính đường tròn ngoại tiếp thì bằng 1313 đường cao.
Mà đường cao thì bằng √3232 cạnh.
Nên cạnh của tam giác gấp 2√323 bán kính, tức là bằng 2√3r23�.
Diện tích 2√3r.3r2=3√3r223�.3�2=33�2.
Để chứng minh diện tích của tam giác đều ngoại tiếp đường tròn bán kính r bằng 3r^2, ta sẽ sử dụng các công thức và tính chất của tam giác đều và đường tròn.
Giả sử tam giác đều ngoại tiếp đường tròn có tâm O và bán kính r. Đường tròn này cắt tam giác đều tại các đỉnh A, B và C.
Để tính diện tích của tam giác đều ABC, ta sẽ sử dụng công thức diện tích tam giác đều:
Diện tích tam giác đều ABC = (cạnh)^2 * sqrt(3) / 4
Với tam giác đều ngoại tiếp đường tròn, cạnh tam giác bằng đường kính của đường tròn, tức là 2r.
Diện tích tam giác đều ABC = (2r)^2 * sqrt(3) / 4
= 4r^2 * sqrt(3) / 4
= r^2 * sqrt(3)
Vậy diện tích của tam giác đều ngoại tiếp đường tròn bán kính r là r^2 * sqrt(3).
Để chứng minh r^2 * sqrt(3) = 3r^2, ta sẽ sử dụng tính chất của căn bậc hai:
sqrt(3) = sqrt(3) * sqrt(1) = sqrt(3 * 1) = sqrt(3) * sqrt(3) / sqrt(3) = 3 / sqrt(3)
Vậy r^2 * sqrt(3) = r^2 * (3 / sqrt(3)) = 3r^2.
Vậy ta đã chứng minh được diện tích của tam giác đều ngoại tiếp đường tròn bán kính r bằng 3r^2.
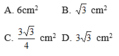
,Gọi độ dài cạnh tam giác là x
Ta có: S=pr=2.3x2=3x
Kẻ MH vuông góc với NP
MH=3r=3.2=6
x=\(\sqrt{48}\)
S=\(\sqrt{432}\)
a=432