K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
D
25 tháng 3 2020
a) Hai mặt phẳng cắt nhau, vì 1: 2: (-1) ≠ 2: 3: (-7)
b) Hai mặt phẳng cắt nhau, vì: 1: (-2): 1 ≠ 2: (-1): 4
c) Hai mặt phẳng song song, vì: 1/2=1/2=1/2 ≠ -1/3
d) Hai mạt phẳng cắt nhau, vì: 3: (-2): 3 ≠ 9: (-6): (-9)
e) Hai mặt phẳng trung nhau, vì: 1/10=-1/(-10)=2/20=-4/(-40).
#rin
GV
Giáo viên Toán
Giáo viên
4 tháng 5 2017
a) \(\int\left(x+\ln x\right)x^2\text{d}x=\int x^3\text{d}x+\int x^2\ln x\text{dx}\)
\(=\dfrac{x^4}{4}+\int x^2\ln x\text{dx}+C\) (*)
Để tính: \(\int x^2\ln x\text{dx}\) ta sử dụng công thức tính tích phân từng phần như sau:
Đặt \(\left\{{}\begin{matrix}u=\ln x\\v'=x^2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u'=\dfrac{1}{x}\\v=\dfrac{1}{3}x^3\end{matrix}\right.\)
Suy ra:
\(\int x^2\ln x\text{dx}=\dfrac{1}{3}x^3\ln x-\dfrac{1}{3}\int x^2\text{dx}\)
\(=\dfrac{1}{3}x^3\ln x-\dfrac{1}{3}.\dfrac{1}{3}x^3\)
Thay vào (*) ta tính được nguyên hàm của hàm số đã cho bằng:
(*) \(=\dfrac{1}{3}x^3-\dfrac{1}{3}x^3\ln x+\dfrac{1}{9}x^3+C\)
\(=\dfrac{4}{9}x^3-\dfrac{1}{3}x^3\ln x+C\)
GV
Giáo viên Toán
Giáo viên
4 tháng 5 2017
b) Đặt \(\left\{{}\begin{matrix}u=x+\sin^2x\\v'=\sin x\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}u'=1+2\sin x.\cos x\\v=-\cos x\end{matrix}\right.\)
Ta có:
\(\int\left(x+\sin^2x\right)\sin x\text{dx}=-\left(x+\sin^2x\right)\cos x+\int\left(1+2\sin x\cos^2x\right)\text{dx}\)
\(=-\left(x+\sin^2x\right)\cos x+\int\cos x\text{dx}+2\int\sin x.\cos^2x\text{dx}\)
\(=-\left(x+\sin^2x\right)\cos x+\sin x-2\int\cos^2x.d\left(\cos x\right)\)
\(=-\left(x+\sin^2x\right)\cos x+\sin x-2\dfrac{\cos^3x}{3}+C\)
2
18 tháng 11 2023
`a)TXĐ:R\\{1;1/3}`
`y'=[-4(6x-4)]/[(3x^2-4x+1)^5]`
`b)TXĐ:R`
`y'=2x. 3^[x^2-1] ln 3-e^[-x+1]`
`c)TXĐ: (4;+oo)`
`y'=[2x-4]/[x^2-4x]+2/[(2x-1).ln 3]`
`d)TXĐ:(0;+oo)`
`y'=ln x+2/[(x+1)^2].2^[[x-1]/[x+1]].ln 2`
`e)TXĐ:(-oo;-1)uu(1;+oo)`
`y'=-7x^[-8]-[2x]/[x^2-1]`
AH
Akai Haruma
Giáo viên
18 tháng 11 2023
Lời giải:
a.
$y'=-4(3x^2-4x+1)^{-5}(3x^2-4x+1)'$
$=-4(3x^2-4x+1)^{-5}(6x-4)$
$=-8(3x-2)(3x^2-4x+1)^{-5}$
b.
$y'=(3^{x^2-1})'+(e^{-x+1})'$
$=(x^2-1)'3^{x^2-1}\ln 3 + (-x+1)'e^{-x+1}$
$=2x.3^{x^2-1}.\ln 3 -e^{-x+1}$
c.
$y'=\frac{(x^2-4x)'}{x^2-4x}+\frac{(2x-1)'}{(2x-1)\ln 3}$
$=\frac{2x-4}{x^2-4x}+\frac{2}{(2x-1)\ln 3}$
d.
\(y'=(x\ln x)'+(2^{\frac{x-1}{x+1}})'=x(\ln x)'+x'\ln x+(\frac{x-1}{x+1})'.2^{\frac{x-1}{x+1}}\ln 2\)
\(=x.\frac{1}{x}+\ln x+\frac{2}{(x+1)^2}.2^{\frac{x-1}{x+1}}\ln 2\\ =1+\ln x+\frac{2^{\frac{2x}{x+1}}\ln 2}{(x+1)^2}\)
e.
\(y'=-7x^{-8}-\frac{(x^2-1)'}{x^2-1}=-7x^{-8}-\frac{2x}{x^2-1}\)
TT
1
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 11 2021
\(y'=\dfrac{-2-m}{\left(x-1\right)^2}.e^{\dfrac{2x+m}{x-1}}\)
\(\Rightarrow\) Hàm đơn điệu trên miền xác định
TH1: \(\left\{{}\begin{matrix}-2-m< 0\\y\left(2\right)=e^5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>-2\\\dfrac{m+4}{1}=5\end{matrix}\right.\) \(\Rightarrow m=1\)
TH2: \(\left\{{}\begin{matrix}-2-m>0\\y\left(4\right)=5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< -2\\\dfrac{m+8}{3}=5\end{matrix}\right.\) \(\Rightarrow\) ko tồn tại m thỏa mãn
Vậy \(m=1\)
CM
11 tháng 4 2019
Chọn B
Hàm số đồng biến khi a > 1.
Viết lại các hàm số về dạng hàm số mũ y = a x :
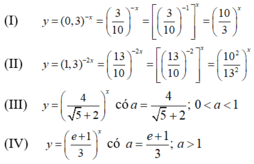
Trong bốn cơ số ta thấy chỉ có hai cơ số lớn hơn 1 là
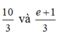
Do đó chỉ có hai hàm số (I) và (IV) là đồng biến trên R
NP
1
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 6 2020
\(\left\{{}\begin{matrix}z'_x=-2x.e^{y-x^2+5}+8x^3=0\\z'_y=e^{y-x^2+5}-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\left(8x^2-2e^{y-x^2+5}\right)=0\\y-x^2+5=0\end{matrix}\right.\)
TH1: \(\left\{{}\begin{matrix}x=0\\y-x^2+5=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=0\\y=-5\end{matrix}\right.\)
Th2: \(\left\{{}\begin{matrix}4x^2=e^{y-x^2+5}\\y-x^2+5=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}4x^2=1\\y-x^2+5=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\frac{1}{2}\\y=-\frac{19}{4}\end{matrix}\right.\) hoặc \(\left\{{}\begin{matrix}x=-\frac{1}{2}\\y=-\frac{19}{4}\end{matrix}\right.\)
Ta có các điểm dừng: \(M\left(0;-5\right)\) ; \(N\left(\frac{1}{2};-\frac{19}{4}\right)\) ; \(P\left(-\frac{1}{2};-\frac{19}{4}\right)\)
\(z''_{xx}=\left(4x^2-2\right)e^{y-x^2+5}+24x^2\)
\(z''_{xy}=-2x.e^{y-x^2+5}\) ; \(z''_{yy}=e^{y-x^2+5}\)
Tại M: \(A=-2\) ; \(B=0\) ; \(C=1\Rightarrow B^2-AC=2>0\Rightarrow M\) không phải cực trị
Tại N: \(A=5>0\) ; \(B=-1\) ; \(C=1\Rightarrow B^2-AC=-4< 0\Rightarrow\) hàm đạt cực tiểu tại N
Tại P: \(A=5>0\) ; \(B=1\) ; \(C=1\Rightarrow B^2-AC=-4< 0\Rightarrow\) hàm đạt cực tiểu tại P
