Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Xét tam giác ABD và tam giác ACE có
góc ADB = góc AEC = 90 độ
AB=AC
góc A: chung
=> tam giác ABD = tam giác ACE (cạnh huyền - góc nhọn)
=> BD=CE và AD=AE
b) Vì AB=AC và AE=AD => AB-AE=AC-AD => BE=CD
Xét tam giác OEB và tam giác ODC có
góc OEB = góc ODC = 90 độ
BE=CD
góc BOE = góc COD (đối đỉnh)
=> tam giác OEB = tam giác ODC => OB=OC
c) Xét tam giác AOB và tam giác AOC có
AB=AC
OB=OC
AO: cạnh chung
=> tam giác AOB = tam giác AOC (c.c.c)
=> góc OAB=góc OAC
=> AO la tia phân giác góc BAC
Bài mk lm như dzị ak
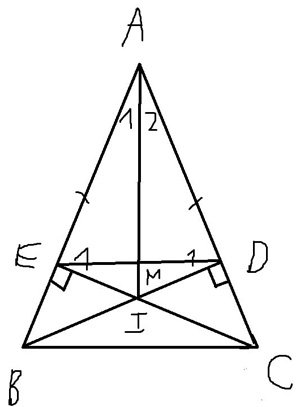a, tg ADB và tg AEC có^E1 = ^D1 = 90 độ
AB = AC
^A chung
=> tg ADB = tg AEC
=> AD = AE
=> tg ADE cân
b, tg ABI và tg ACI có
^E1 = ^D1 = 90 độ
AI chung
AB = AC
=> tg ABI = tg ACI
=> ^A1 = ^A2 ( góc t/ứ)
=> IB = IC ( cạnh t/ứ)
=> tg IBC cân
c, vì ^A1 = ^A2 ( câu b )
=> AI là tpg của góc EAD
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
góc A chung
Do đó; ΔADB=ΔAEC
=>AD=AE
b: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
c: Xét ΔIBC có góc IBC=góc ICB
nên ΔiBC cân tại I
=>IB=IC
d: AB=AC
IB=IC
=>AI là trung trực của BC
=>AI vuông góc với BC
Dễ mà :
Gợi ý ta sẽ áp dụng hệ quả là : Trong một tam giác vuông thì Cạnh huyền luôn lớn hơn Cạnh góc vuông
Giải
a , Xét \(\Delta BAD\)và \(\Delta BED\)có :
AB = BE ( gt )
BD chung
\(\widehat{ABD}=\widehat{DBE}\)( BD là đường phân giác \(\widehat{B}\))
\(\Rightarrow\text{}\text{}\text{}\text{}\text{}\text{}\Delta ABD=\Delta BDE\left(c.g.c\right)\)
b , Có \(\Delta ABD=\Delta BDE\)
\(\Rightarrow\widehat{E}=\widehat{A}=90^0\)( 2 góc tương ứng )
Ta có : \(\hept{\begin{cases}\widehat{AFD}+\widehat{ADF}=90^0\\\widehat{ECD}+\widehat{EDC}=90^0\\\widehat{ADF}=\widehat{EDC}\left(đđ\right)\end{cases}}\)
\(\Rightarrow\widehat{AFD}=\widehat{DCE}\)
Xét \(\Delta ADF\)vuông tại A và \(\Delta EDC\)vuông tại E có :
\(\hept{\begin{cases}\text{ AF = EC ( gt )}\\\widehat{AFD\: }=\widehat{DCE}\left(cmt\right)\end{cases}\Rightarrow\Delta ADF=\Delta EDC\left(cgv.gn\right)}\)
\(\Rightarrow DF=DC\)( 2 cạnh tương ứng )
c , Có \(D\in AC\)( BD cắt AC tại D )
\(\widehat{EDC}+\widehat{ADE}=180^0\)
Mà \(\widehat{ADF}=\widehat{EDC}\)( 2 góc đối đỉnh )
\(\Rightarrow\widehat{ADF}+\widehat{ADE}=180^0\)
\(\Rightarrow\widehat{EDF}=180^0\)
\(\Rightarrow\)E , D , F cùng nằm trên 1 đường thẳng .
a) Cm BD = CE
\(\Delta ABC\)có AB = AC => \(\Delta ABC\)là tam giác cân tại A
Xét \(\Delta EBC\)và \(\Delta DCB\)có
Góc B = Góc C (Vì \(\Delta ABC\)cân)
BC : cạnh huyền chung
=> \(\Delta EBC=\Delta DCB\)(cạnh huyền - góc nhọn)
=> BD = CE (cạnh tương ứng) => ĐPCM
b) CM: EI = DI
Xét \(\Delta AHB\)và \(\Delta AHC\)có \(\hept{\begin{cases}AB=AC\left(gt\right)\\\widehat{B}=\widehat{C}\left(gt\right)\\BH=HC\left(gt\right)\end{cases}\Rightarrow\Delta AHB=\Delta AHC\left(c.g.c\right)}\)
=> \(\widehat{BAH}=\widehat{CAH}\)(góc tương ứng)
xét tam giác vuông AIE và tam giác vuông AID có
AI là cạnh huyền chung
\(\widehat{BAH}=\widehat{CAH}\) ( cmt)
do đó \(\Delta AIE=\Delta AID\) ( cạnh huyền - góc nhọn )
suy ra EI = ID ( 2 cạnh tương ứng )
c) \(\widehat{BAH}=\widehat{CAH}\) mà tia AH nằm giữa tia AB và AC nên AH là phân giác \(\widehat{BAC}\) (1)
\(\Delta AIE=\Delta AID\) suy ra \(\widehat{EAI}=\widehat{DAI}\) ( 2 góc tương ứng )
mà tia AI nằm giữa 2 tia AE và AD suy ra AI là phân giác \(\widehat{EAD}\) hay \(\widehat{BAD}\) (2)
từ (1) và (2) suy ra ba điểm A;I:H thẳng hàng
a) Ta có: ΔADB vuông tại D(BD là đường cao ứng với cạnh AC)
nên AB là cạnh huyền(AB là cạnh đối diện với góc vuông \(\widehat{ADB}\))
Suy ra: AB là cạnh lớn nhất trong ΔADB
hay AB>DB
b)
Xét ΔACE vuông tại E có AC là cạnh huyền(AC là cạnh đối diện với \(\widehat{AEC}=90^0\))
nên AC là cạnh lớn nhất trong ΔACE(Định lí tam giác vuông)
hay AC>CE(đpcm)