K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 7 2021
\(A=\dfrac{\sqrt{20}-6}{\sqrt{14-6\sqrt{5}}}-\dfrac{\sqrt{20}-\sqrt{28}}{\sqrt{12-2\sqrt{35}}}=\dfrac{-2\left(3-\sqrt{5}\right)}{\sqrt{\left(3-\sqrt{5}\right)^2}}+\dfrac{2\left(\sqrt{7}-\sqrt{5}\right)}{\sqrt{\left(\sqrt{7}-\sqrt{5}\right)^2}}\)
\(=\dfrac{-2\left(3-\sqrt{5}\right)}{3-\sqrt{5}}+\dfrac{2\left(\sqrt{7}-\sqrt{5}\right)}{\sqrt{7}-\sqrt{5}}=-2+2=0\)
\(B=\sqrt{\dfrac{\left(9-4\sqrt{3}\right)\left(6-\sqrt{3}\right)}{\left(6-\sqrt{3}\right)\left(6+\sqrt{3}\right)}}-\sqrt{\dfrac{\left(3+4\sqrt{3}\right)\left(5\sqrt{3}+6\right)}{\left(5\sqrt{3}-6\right)\left(5\sqrt{3}+6\right)}}\)
\(=\sqrt{\dfrac{66-33\sqrt{3}}{33}}-\sqrt{\dfrac{78+39\sqrt{3}}{39}}=\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{4-2\sqrt{3}}-\sqrt{4+2\sqrt{3}}\right)=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{\left(\sqrt{3}+1\right)^2}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{3}-1-\sqrt{3}-1\right)=-\sqrt{2}\)
28 tháng 7 2021
a) Ta có: \(A=\dfrac{\sqrt{10}-3\sqrt{2}}{\sqrt{7-3\sqrt{5}}}-\dfrac{\sqrt{10}-\sqrt{14}}{\sqrt{6-\sqrt{35}}}\)
\(=\dfrac{2\sqrt{5}-6}{3-\sqrt{5}}-\dfrac{2\sqrt{5}-2\sqrt{7}}{\sqrt{7}-\sqrt{5}}\)
\(=\dfrac{\left(2\sqrt{5}-6\right)\left(3+\sqrt{5}\right)}{4}-\dfrac{\left(2\sqrt{5}-2\sqrt{7}\right)\left(\sqrt{7}+\sqrt{5}\right)}{2}\)
\(=\dfrac{\left(\sqrt{5}-3\right)\left(3+\sqrt{5}\right)-\left(2\sqrt{5}-2\sqrt{7}\right)\left(\sqrt{7}+\sqrt{5}\right)}{2}\)
\(=\dfrac{5-9-2\left(5-7\right)}{2}\)
\(=\dfrac{-4-2\cdot\left(-2\right)}{2}\)
\(=0\)
HK
3
31 tháng 10 2021
Bạn ơi, làm như vậy thì quá ngắn rồi ạ, với lại bạn làm thiếu mất đề bài của mình rồi
LV
1
AH
Akai Haruma
Giáo viên
31 tháng 7 2023
Bạn cần viết đầy đủ đề thì mọi người mới giúp được bạn nhé. Đọc đề chỉ có biểu thức không khó hiểu lắm.
S2
1
20 tháng 5 2022
\(\text{Δ}=\left(-3\right)^2-4\cdot\left(2m+1\right)\)
=9-8m-4=-8m+5
Để phương trình có nghiệm kép thì -8m+5=0
hay m=5/8
Pt trở thành \(x^2-3x+\dfrac{9}{4}=0\)
hay x=3/2
AH
Akai Haruma
Giáo viên
8 tháng 5 2022
Lời giải:
ĐKXĐ: $x>0; x\neq 1$
\(P=\left[\frac{x}{\sqrt{x}(\sqrt{x}-1)}-\frac{1}{\sqrt{x}(\sqrt{x}-1)}\right]:\left[\frac{\sqrt{x}-1}{(\sqrt{x}+1)(\sqrt{x}-1)}+\frac{2}{(\sqrt{x}-1)(\sqrt{x}+1)}\right]\)
\(=\frac{x-1}{\sqrt{x}(\sqrt{x}-1)}:\frac{\sqrt{x}+1}{(\sqrt{x}-1)(\sqrt{x}+1)}\)
\(=\frac{(\sqrt{x}-1)(\sqrt{x}+1)}{\sqrt{x}(\sqrt{x}-1)}:\frac{1}{\sqrt{x}-1}=\frac{\sqrt{x}+1}{\sqrt{x}}.(\sqrt{x}-1)=\frac{x-1}{\sqrt{x}}\)
b.
$x=7-4\sqrt{3}=(2-\sqrt{3})^2\Rightarrow \sqrt{x}=2-\sqrt{3}$
Khi đó:
$P=\frac{6-4\sqrt{3}}{2-\sqrt{3}}=-2\sqrt{3}$
c.
$P=\frac{x-1}{\sqrt{x}}=\frac{3}{2}$
$\Rightarrow 2(x-1)=3\sqrt{x}$
$\Leftrightarrow 2x-3\sqrt{x}-2=0$
$\Leftrightarrow (\sqrt{x}-2)(2\sqrt{x}+1)=0$
$\Rightarrow x=4$ (tm)
AH
Akai Haruma
Giáo viên
8 tháng 5 2022
Lời giải:
ĐKXĐ: $x>0; x\neq 1$
\(P=\left[\frac{x}{\sqrt{x}(\sqrt{x}-1)}-\frac{1}{\sqrt{x}(\sqrt{x}-1)}\right]:\left[\frac{\sqrt{x}-1}{(\sqrt{x}+1)(\sqrt{x}-1)}+\frac{2}{(\sqrt{x}-1)(\sqrt{x}+1)}\right]\)
\(=\frac{x-1}{\sqrt{x}(\sqrt{x}-1)}:\frac{\sqrt{x}+1}{(\sqrt{x}-1)(\sqrt{x}+1)}\)
\(=\frac{(\sqrt{x}-1)(\sqrt{x}+1)}{\sqrt{x}(\sqrt{x}-1)}:\frac{1}{\sqrt{x}-1}=\frac{\sqrt{x}+1}{\sqrt{x}}.(\sqrt{x}-1)=\frac{x-1}{\sqrt{x}}\)
b.
$x=7-4\sqrt{3}=(2-\sqrt{3})^2\Rightarrow \sqrt{x}=2-\sqrt{3}$
Khi đó:
$P=\frac{6-4\sqrt{3}}{2-\sqrt{3}}=-2\sqrt{3}$
c.
$P=\frac{x-1}{\sqrt{x}}=\frac{3}{2}$
$\Rightarrow 2(x-1)=3\sqrt{x}$
$\Leftrightarrow 2x-3\sqrt{x}-2=0$
$\Leftrightarrow (\sqrt{x}-2)(2\sqrt{x}+1)=0$
$\Rightarrow x=4$ (tm)
3 tháng 4 2023
a: góc APH=góc APK=90 độ
gó AEH=90 độ
=>góc APH=góc AEH=90 độ
=>APFE nội tiếp
b: góc AFH=góc AEH=90 độ
=>AFHE nội tiếp
=>A,P,F,E,H cùng thuộc 1 đường tròn
=>góc PFx=góc PEH
góc PEB=góc PEx+góc xFB=90 độ+góc PEx
góc PEC=góc PEH+góc HEC=góc PEH+90 độ
=>góc PEB=góc PEC
Xét ΔPBF và ΔPCE có
góc PBF=góc PCE
góc PFB=góc PEC
=>ΔPBF đồng dạng với ΔPCE
=>PB/PC=PF/PE
=>PB*PE=PC*PF
HK
1
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 5 2021
\(Q=\dfrac{\sqrt{x}-3}{\sqrt{x}-1}=\dfrac{\sqrt{x}-1-2}{\sqrt{x}-1}=1-\dfrac{2}{\sqrt{x}-1}\)
\(\Rightarrow\sqrt{x}-1=Ư\left(2\right)=\left\{-2;-1;1;2\right\}\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}-1=-2\\\sqrt{x}-1=-1\\\sqrt{x}-1=1\\\sqrt{x}-1=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\sqrt{x}=-1\left(vn\right)\\\sqrt{x}=0\\\sqrt{x}=2\\\sqrt{x}=3\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=4\\x=9\end{matrix}\right.\)
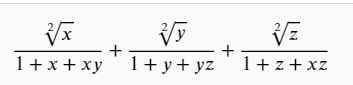
Bài 5:
a: Phương trình hoành độ giao điểm là:
\(x^2-2x-m^2-1=0\)
\(\text{Δ}=\left(-2\right)^2-4\cdot\left(-m^2-1\right)\)
\(=4+4m^2+4=4m^2+8>0\)
Vậy: (P) cắt (d) tại hai điểm phân biệt
b: Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-m^2-1\end{matrix}\right.\)
Theo đề, ta có: \(x_A^2+x_B^2=14\)
\(\Leftrightarrow4-2\left(-m^2-1\right)=14\)
\(\Leftrightarrow2m^2=8\)
hay \(m\in\left\{2;-2\right\}\)
còn bài 3 và bài 4 thí sao hả bạn