Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta lập bảng xét dấu
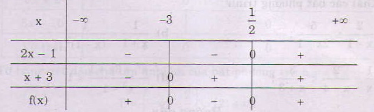
Kết luận: f(x) < 0 nếu - 3 < x <
f(x) = 0 nếu x = - 3 hoặc x =
f(x) > 0 nếu x < - 3 hoặc x > .
b) Làm tương tự câu a).
f(x) < 0 nếu x ∈ (- 3; - 2) ∪ (- 1; +∞)
f(x) = 0 với x = - 3, - 2, - 1
f(x) > 0 với x ∈ (-∞; - 3) ∪ (- 2; - 1).
c) Ta có: f(x) =
Làm tương tự câu b).
f(x) không xác định nếu x = hoặc x = 2
f(x) < 0 với x ∈ ∪
f(x) > 0 với x ∈ ∪ (2; +∞).
d) f(x) = 4x2 – 1 = (2x - 1)(2x + 1).
f(x) = 0 với x =
f(x) < 0 với x ∈
f(x) > 0 với x ∈ ∪

b: \(f\left(-x\right)=\dfrac{\left|-x+1\right|+\left|-x-1\right|}{\left|-x+1\right|-\left|-x-1\right|}\)
\(=\dfrac{\left|x-1\right|+\left|x+1\right|}{\left|x-1\right|-\left|x+1\right|}\)
=-f(x)
Vậy: f(x) là hàm số lẻ

Đầu tiên ta để ý rằng hàm trên và hàm dưới đều có dạng rất giống nhau, biểu thức x trong ngoặc đầu tiên cộng 2 lần biểu thức x trong ngoặc thứ 2 đều bằng 1, do đó ta tìm cách đưa hàm pt 2 về dạng của hàm pt 1:
Đặt \(\dfrac{x}{x+1}=2t-1\Rightarrow x=2tx-x+2t-1\Rightarrow x\left(2-2t\right)=2t-1\Rightarrow x=\dfrac{2t-1}{2-2t}\)
\(\Rightarrow\dfrac{1}{2x+2}=\dfrac{1}{\dfrac{2t-1}{1-t}+2}=1-t\) \(\left(t\ne1\right)\)
\(\Rightarrow\) pt dưới trở thành \(f\left(2t-1\right)+2g\left(1-t\right)=3\) hay \(f\left(2x-1\right)+2g\left(1-x\right)=3\)
Ta có hệ:
\(\left\{{}\begin{matrix}f\left(2x-1\right)+g\left(1-x\right)=x+1\\f\left(2x-1\right)+2g\left(1-x\right)=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}g\left(1-x\right)=2-x=1+1-x\\f\left(2x-1\right)=2x-1\end{matrix}\right.\)
Vậy nghiệm của hệ pt là \(\left\{{}\begin{matrix}f\left(x\right)=x\\g\left(x\right)=x+1\end{matrix}\right.\)

a) 3x^3 -10x+3 =(3x-1)(x-3)
| x | -vc | 1/3 | 5/4 | 3 | +vc | |||||||||
| 3x-1 | - | 0 | + | + | + | + | + | |||||||
| x-3 | - | - | - | - | - | 0 | + | |||||||
| 4x-5 | - | - | - | 0 | + | + | + | |||||||
| VT | - | 0 | + | 0 | - | 0 | + |
Kết luận
VT< 0 {dấu "-"} khi x <1/3 hoắc 5/4<x<3
VT>0 {dấu "+"} khi x 1/3<5/4 hoặc x> 3
VT=0 {không có dấu} khi x={1/3;5/4;3}

Hàm xác định trên R
\(f\left(-x\right)=\dfrac{\left|-x+1\right|-\left|-x-1\right|}{\left|-x+2\right|+\left|-x-2\right|}=\dfrac{\left|x-1\right|-\left|x+1\right|}{\left|x+2\right|+\left|x-2\right|}=-f\left(x\right)\)
Hàm đã cho là hàm lẻ

a) miền xác định của \(f\) là \(D=R\backslash\left\{\pm1\right\}\)
\(\text{∀}x\in D\), ta có: \(-x\in D\) và \(f\left(-x\right)=\frac{2x^4-x^2+3}{x^2-2}=f\left(x\right)\)
\(\Rightarrow\) \(f\) là hàm số chẵn
b) Ta có: \(\left|2x+1\right|-\left|2x-1\right|\ne0\)\(\Leftrightarrow\left|2x+1\right|\ne\left|2x-1\right|\)
\(\Leftrightarrow\left(2x+1\right)^2\ne\left(2x-1\right)^2\)
\(\Leftrightarrow x\ne0\)
\(\Rightarrow\) Miền xác định của \(f\) là \(D=R\backslash\left\{0\right\}\)
khi đó \(\text{∀}x\in D\) thì \(-x\in D\) và :
\(f\left(-x\right)=\frac{\left|-2x+1\right|+\left|-2x-1\right|}{\left|-2x+1\right|-\left|-2x-1\right|}\)\(=\frac{\left|2x-1\right|+\left|2x+1\right|}{\left|2x-1\right|-\left|2x+1\right|}\)\(=-\frac{\left|2x+1\right|+\left|2x-1\right|}{\left|2x+1\right|-\left|2x-1\right|}\)
\(=-f\left(x\right)\Rightarrow f\) là hàm số lẻ

c) \(h\left(x\right)=\left(x+1\right)^2+\left(\dfrac{x^2+2x+2}{x+1}\right)^2=\left(x+1\right)^2+\left(x+1+\dfrac{1}{x+1}\right)^2=2\left(x+1\right)^2+\dfrac{1}{\left(x+1\right)^2}+2\ge_{AM-GM}2\sqrt{2}+2\).
Đẳng thức xảy ra khi \(2\left(x+1\right)^2=\dfrac{1}{\left(x+1\right)^2}\Leftrightarrow x=\pm\sqrt{\dfrac{1}{2}}-1\).
b) \(g\left(x\right)=\dfrac{\left(x+2\right)\left(x+3\right)}{x}=\dfrac{x^2+5x+6}{x}=\left(x+\dfrac{6}{x}\right)+5\ge_{AM-GM}2\sqrt{6}+5\).
Đẳng thức xảy ra khi x = \(\sqrt{6}\).
a: \(f\left(-x\right)=\dfrac{-x^3}{\left|x\right|-1}< >f\left(x\right)\)
=>f(x) khôg chẵn cũng ko lẻ
b: \(f\left(-x\right)=\dfrac{\left|-x-1\right|+\left|-x+1\right|}{\left|-2x-1\right|+\left|-2x+1\right|}\)
\(=\dfrac{\left|x+1\right|+\left|x-1\right|}{\left|2x+1\right|+\left|2x-1\right|}=f\left(x\right)\)
=>f(x) là hàm số chẵn