Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) TXĐ: R
y′ = 6x − 24 x 2 = 6x(1 − 4x)
y' = 0 ⇔ 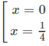
y' > 0 trên khoảng (0; 1/4) , suy ra y đồng biến trên khoảng (0; 1/4)
y' < 0 trên các khoảng ( - ∞ ; 0 ); (14; + ∞ ), suy ra y nghịch biến trên các khoảng ( - ∞ ;0 ); (14; + ∞ )
b) TXĐ: R
y′ = 16 + 4x − 16 x 2 − 4 x 3 = −4(x + 4)( x 2 − 1)
y' = 0 ⇔ 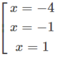
Bảng biến thiên:
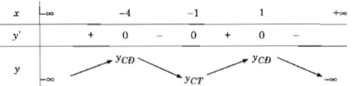
Vậy hàm số y đã cho đồng biến trên các khoảng ( - ∞ ; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1; + ∞ )
c) TXĐ: R
y′ = 3 x 2 − 12x + 9
y' = 0
y' > 0 trên các khoảng ( - ∞ ; 1), (3; + ∞ ) nên y đồng biến trên các khoảng ( - ∞ ; 1), (3; + ∞ )
y'< 0 trên khoảng (1; 3) nên y nghịch biến trên khoảng (1; 3)
d) TXĐ: R
y′ = 4 x 3 + 16 = 4x( x 2 + 4)
y' = 0 ⇔ 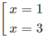
y' > 0 trên khoảng (0; + ∞ ) ⇒ y đồng biến trên khoảng (0; + ∞ )
y' < 0 trên khoảng ( - ∞ ; 0) ⇒ y nghịch biến trên khoảng ( - ∞ ; 0)

TXĐ: R
y′ = 16 + 4x − 16 x 2 − 4 x 3 = −4(x + 4)( x 2 − 1)
y' = 0 ⇔ 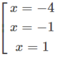
Bảng biến thiên:
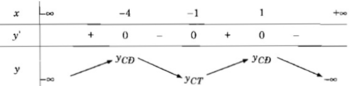
Vậy hàm số y đã cho đồng biến trên các khoảng (- ∞ ; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1; + ∞ )

TXĐ: R
y′ = 4 x 3 + 16 = 4x( x 2 + 4)
y' = 0 ⇔ 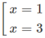
y' > 0 trên khoảng (0; + ∞ ) ⇒ y đồng biến trên khoảng (0; + ∞ )
y' < 0 trên khoảng (- ∞ ; 0) ⇒ y nghịch biến trên khoảng (- ∞ ; 0)

Tập xác định: D = R
y'= -3x2 + 2x
y' = 0 ⇔ -3x2 + 2x = 0 ⇔ x.(-3x + 2) = 0 ⇔ 
Bảng biến thiên:
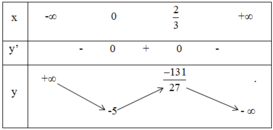
Vậy hàm số nghịch biến trong các khoảng (-∞ ; 0) và (2/3 ; + ∞), đồng biến trong khoảng (0 ; 2/3).

TXĐ: R
y′ = 3 x 2 − 12x + 9
y' = 0
y' > 0 trên các khoảng (- ∞ ; 1), (3; + ∞ ) nên y đồng biến trên các khoảng (- ∞ ; 1), (3; + ∞ )
y'< 0 trên khoảng (1; 3) nên y nghịch biến trên khoảng (1; 3)

Tập xác định: D = R
y'= 4x3 – 4x.
y' = 0 ⇔ 4x3 – 4x = 0 ⇔ 4x.(x – 1)(x + 1) = 0 ⇔ 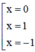
Bảng biến thiên:
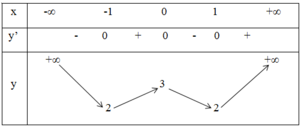
Vậy hàm số nghịch biến trong các khoảng (-∞ ; -1) và (0 ; 1); đồng biến trong các khoảng (-1 ; 0) và (1; +∞).

Tập xác định : D = R
y' = 3 – 2x
y’ = 0 ⇔ 3 – 2x = 0 ⇔ x = 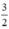
Ta có bảng biến thiên:
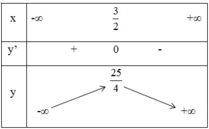
Vậy hàm số đồng biến trong khoảng (-∞; 3/2) và nghịch biến trong khoảng (3/2 ; + ∞).
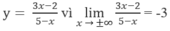
1. a) Tập xác định: D = R;
y' = 3 – 2x => y' = 0 ⇔ x = 3/2
Ta có Bảng biến thiên:
Hàm số đồng biến trên khoảng (-∞; 3/2); nghịch biến trên khoảng (3/2; +∞).
b) Tập xác định: D = R;
y' = x2 + 6x – 7 => y' = 0 ⇔ x = 1, x = -7.
Bảng biến thiên:
Hàm số đồng biến trên các khoảng (-∞; -7), (1; +∞); nghịch biến trên các khoảng (-7; 1).
c) Tập xác định: D = R.
y' = 4x3 – 4x = 4x(x2 – 1) => y' = 0 ⇔ x = -1, x = 0, x = 1.
Bảng biến thiên: (Học sinh tự vẽ)
Hàm số đồng biến trên các khoảng (-1; 0), (; +∞); nghịch biến trên các khoảng (-∞; -1), (0; 1).
d) Tập xác định: D = R.
y' = -3x2 + 2x => y' = 0 ⇔ x = 0, x = 2/3.
Bảng biến thiên:
Hàm số đồng biến trên khoảng (0; 2/3); nghịch biến trên các khoảng (-∞; 0), (2/3; +∞).