Xét dấu biểu thức sau: f ( x ) = 2 x + 1 x

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

31 tháng 5 2018

Xét dấu biểu thức sau: f ( x ) = 2 x + 1 x - 1 x + 2

#Toán lớp 10

Cao Minh Tâm

31 tháng 5 2018

Giải sách bài tập Toán 10 | Giải sbt Toán 10

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

KhánhLinh Nguyễn

27 tháng 2 2021

Xét dấu của biểu thức sau : f(x) = (1+x)(x-2)^2(4-x)

#Toán lớp 10

Đỗ Thanh Hải

CTVVIP

27 tháng 2 2021

Xét f(x) = (1+x)(x-2)²(4-x)

f(x) = 0 \(\Leftrightarrow\) x = -1 hoặc x = 2 hoặc x = 4

ta có bảng

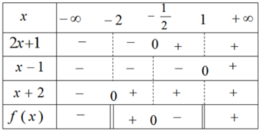
x \(-\infty\) -1 2 4 \(+\infty\)

1+x - 0 + | + | +

(x-2)² + | + 0 + | +

4-x + | + | + 0 -

f(x) - 0 + 0 + 0 -

Chúc bn học tốt

Đúng(1)

Mai Lin

12 tháng 4 2021

Bài 3: Xét dấu các biểu thức sau 1/ f(x) = (2x - 1)(x ^ 3 - 1)

. 2 / (f(x)) = (- 2x ^ 2 + 7x + 7)/(x ^ 2 - 3x - 10) - 1

#Toán lớp 10

Pham Trong Bach

8 tháng 2 2019

Xét dấu biểu thức sau: f(x) = (4x - 1)(x + 2)(3x - 5)(-2x + 7)

#Toán lớp 10

Cao Minh Tâm

8 tháng 2 2019

Giải sách bài tập Toán 10 | Giải sbt Toán 10

Đúng(0)

Pham Trong Bach

19 tháng 12 2017

Xét dấu biểu thức sau: f ( x ) = 3 2 x - 1 - 1 x + 2

#Toán lớp 10

Cao Minh Tâm

19 tháng 12 2017

Giải sách bài tập Toán 10 | Giải sbt Toán 10

Đúng(0)

Luân Đinh Tiến

13 tháng 1 2021

Xét dấu biểu thức sau đây:\(f\left(x\right)=\) \(\dfrac{2x+3}{x+1}+\dfrac{x+6}{-3x-2}\)

#Toán lớp 10

Minh Thiên

3 tháng 2 2021

Xét dấu các biểu thức sau: a) f(x)= (x-2).(x+1)/3x -1 b) f(x)= 1-4x /2x-3 c) f(x)= 3x (6 -2x)/5x-4 d) f(x)= -4/3x+1 - 3/2-x e) f(x)= 2x-5/(3x+1) (2-4x)

#Toán lớp 10

Nguyen Yen Chi

29 tháng 3 2021

Xét các dấu biểu thức : a) f(x) = (3-x)(x+2) b) f(x) = (x-1)(x^2-6x-7) c) f(x) = -3x^2 + x + 2

#Toán lớp 10

Pham Trong Bach

10 tháng 9 2017

Xét dấu biểu thức sau: f(x) = (-2x + 3)(x - 2)(x + 4)

#Toán lớp 10

Cao Minh Tâm

10 tháng 9 2017

Giải sách bài tập Toán 10 | Giải sbt Toán 10

Đúng(0)

Pham Trong Bach

3 tháng 5 2018

Xét dấu của các biểu thức sau : f(x) = ( -x2+x-1)(6x2-5x+1) A. f(x) > 0 khi và chỉ khi x ∈ 1 3 ; 1 2 B. f(x) < 0 khi và chỉ khi x ∈ 1 3 ; 1 2 C. f(x)>0 khi và chỉ khi x ∈ - ∞ ; 1 3 ∪ 1 2 ; + ∞ D. f(x)< 0 khi và chỉ khi x ∈ - ∞ ; 1 ...

Đọc tiếp

#Toán lớp 10

Cao Minh Tâm

3 tháng 5 2018

Chọn A

Ta có –x²+x-1= 0 vô nghiệm,

6x²- 5x+1= 0 khi x= ½ hoặc x= 1/3

Bảng xét dấu

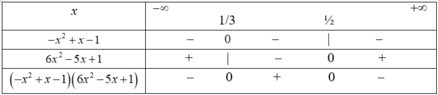
Suy ra f(x) > 0 khi và chỉ khi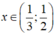

Và f( x)< 0 khi và chỉ khi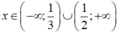

Đúng(0)

Quoc Tran Anh Le

Giáo viên

26 tháng 9 2023

Biểu thức nào sau đây là tam thức bậc hai? Nếu là tam thức bậc hai, hãy xét dấu của nó tại \(x = 1\).

a) \(f\left( x \right) = 2{x^2} + x - 1\);

b) \(g\left( x \right) = - {x^4} + 2{x^2} + 1\)

c) \(h\left( x \right) = - {x^2} + \sqrt 2 .x - 3\)

#Toán lớp 10

Hà Quang Minh

Giáo viên

26 tháng 9 2023

a) Biểu thức \(f\left( x \right) = 2{x^2} + x - 1\) là một tam thức bậc hai

\(f\left( 1 \right) = {2.1^2} + 1 - 1 = 2 > 0\) nên \(f\left( x \right)\) dương tại \(x = 1\)

b) Biểu thức \(g\left( x \right) = - {x^4} + 2{x^2} + 1\) không phải là một tam thức bậc hai

c) Biểu thức \(h\left( x \right) = - {x^2} + \sqrt 2 .x - 3\) là một tam thức bậc hai

\(h\left( 1 \right) = - {1^2} + \sqrt 2 .1 - 3 = \sqrt 2 - 4 < 0\) nên \(h\left( x \right)\) âm tại \(x = 1\)

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP