Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình \({x^2} - 2x - 3 = 0\) có 2 nghiệm phân biệt \({x_1} = - 1,{x_2} = 3\)
Có \(a = 1 > 0\) nên
\(f\left( x \right) = {x^2} - 2x - 3 > 0\) khi và chỉ khi \(x \in \left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right)\)
=> Phát biểu a) đúng.
\(f\left( x \right) = {x^2} - 2x - 3 < 0\) khi và chỉ khi \(x \in \left( { - 1;3} \right)\)
=> Phát biểu b) sai vì khi x=-1 hoặc x=3 thì \({x^2} - 2x - 3 = 0\) (không nhỏ hơn 0).

a: TXĐ: D=R
b: \(f\left(-1\right)=\dfrac{2}{-1-1}=\dfrac{2}{-2}=-1\)
\(f\left(0\right)=\sqrt{0+1}=1\)
\(f\left(1\right)=\sqrt{1+1}=\sqrt{2}\)
\(f\left(2\right)=\sqrt{3}\)

f(x)>0 với mọi x khi và chỉ khi: \(\left\{{}\begin{matrix}\text{Δ}< 0\\a>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b^2-4ac< 0\\a>0\end{matrix}\right.\)

Lời giải:
Do $-3<-1$ nên:
$f(-3)=3(-3)^2-(-3)+1=31$
Do $0> -1$ nên:
$f(0)=\sqrt{0+1}-2=-1$
$\Rightarrow f(-3)+f(0)=31+(-1)=30$

Để phương trình đã cho có 2 nghiệm trái dấu khi ac < 0
Hay (m2+ 1). (- 2m + 3 )< 0
Lại có, m2 + 1 > 0 với mọi m
Suy ra: -2m + 3 < 0 ⇔ m > 3 2

Ở góc trái khung soạn thảo có hỗ trợ viết công thức toán (biểu tượng $\sum$). Bạn viết lại đề bằng cách này để được hỗ trợ tốt hơn.

a: Khi m=0 thì f(x)=-x2-x+1
f(x)<0
\(\Leftrightarrow-x^2-x+1< 0\)
\(\Leftrightarrow x^2+x-1>0\)
\(\Leftrightarrow\left(x+\dfrac{1}{2}\right)^2-\dfrac{5}{4}>0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{2}>\dfrac{\sqrt{5}}{2}\\x+1< -\dfrac{\sqrt{5}}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>\dfrac{\sqrt{5}-1}{2}\\x< \dfrac{-\sqrt{5}-1}{2}\end{matrix}\right.\)
b: TH1: m=1
Pt sẽ là -2x+2=0
=>-2x=-2
hay x=1(loại)
TH2: m<>1
\(\text{Δ}=\left(m+1\right)^2-4\left(m-1\right)\left(m+1\right)\)
\(=m^2+2m+1-4m^2+4=-3m^2+2m+5\)
Để f(x) vô nghiệm thì \(3m^2-2m-5>0\)
\(\Leftrightarrow\left(3m-5\right)\left(m+1\right)>0\)
=>m>5/3 hoặc m<-1

Chọn A
Ta có –x2+x-1= 0 vô nghiệm,
6x2- 5x+1= 0 khi x= ½ hoặc x= 1/3
Bảng xét dấu
Suy ra f(x) > 0 khi và chỉ khi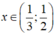
Và f( x)< 0 khi và chỉ khi