NM
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NS
1
AH
Akai Haruma
Giáo viên
23 tháng 5 2022
Lời giải:
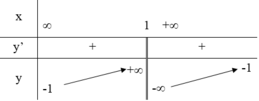
TXĐ: (-\infty; -1)\cup (-1;+\infty)$
$y'=\frac{1}{(x+1)^2}-2$
$y'>0\Leftrightarrow (x+1)^2< \frac{1}{2}\Leftrightarrow \frac{-1}{\sqrt{2}}-1< x< \frac{1}{\sqrt{2}}-1$
$y'< 0\Leftrightarrow (x+1)^2> \frac{1}{2}\Leftrightarrow x> \frac{1}{\sqrt{2}}-1$ hoặc $x< \frac{-1}{\sqrt{2}}-1$
Vậy hàm số:
Đồng biến trên $(\frac{-1}{\sqrt{2}}-1; \frac{1}{\sqrt{2}}-1)$ và nghịch biến trên $(\frac{1}{\sqrt{2}}-1; +\infty)\cup (-\infty; \frac{-1}{\sqrt{2}}-1)$
PT
0
CM
6 tháng 4 2019
Chọn B
Đặt 
Bài toán quy về tìm giá trị lớn nhất của hàm số y = f(t) trên đoạn [-2;0].
Từ bảng biến thiên ta có giá trị lớn nhất của hàm số y = f(t) trên đoạn [-2;0] là 3.
Vậy giá trị lớn nhất của hàm số f(sin x -1) bằng 3.
7 tháng 6 2021
\(\left(\frac{2x-1}{x+2}\right)'=\frac{5}{\left(x+2\right)^2}>0\)
Vậy hàm số \(y=\frac{2x-1}{x+2}\) đồng biến trên R. Chọn A.
DD
Đoàn Đức Hà
Giáo viên
7 tháng 6 2021
A. là hàm phân thức bậc nhất trên bậc nhất nên không đồng biến trên \(ℝ\).
B., D. là đa thức, có hệ số cao nhất âm nên cũng không thể đồng biến trên \(ℝ\).
C>: \(\left(x^3+2x+1\right)'=3x^2+2>0,\forall x\inℝ\).
Ta chọn C.
ta tính \(y'=3x^2-4x+1\)
\(y'=0\Rightarrow3x^2-4x+1=0\Rightarrow x=1;x=\frac{1}{3}\)
ta có
ta có trong khoảng 2 nghiệm thì y' cùng dấu với hệ số a, ngoài khoảng 2 nghiệm trái dấu với hệ số a
suy ra f'(x)>0 với \(x\in\left(-\infty;\frac{1}{3}\right)\cup\left(1;+\infty\right)\) suy ra hàm số đồng biến trên \(\left(-\infty;\frac{1}{3}\right)\cup\left(1;+\infty\right)\)
lại có f'(x)<0 với \(x\in\left(\frac{1}{3};1\right)\) suy ra hàm số nghịch biến trên \(\left(\frac{1}{3};1\right)\)