K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
2
TP
19 tháng 4 2017
a) Hai đường thẳng a và b cùng vuông góc với đường thẳng MN nên a // b.
b) Ta có góc MPQ = góc Q1 = 50o (so le trong vì a // b)
mà góc Q1 + Q2 = 180o (kề bù)
=> Q2 = 180o - 50o = 130o
Vậy góc NQP = 130o.
HS
0
10 tháng 12 2021
Nếu a ⊥ b và b ⊥ c thì ..a//c.. (từ vuông góc đến song song)
Nếu a⊥b và b//c thì..a⊥c.. (từ vuông góc đến song song)
Nếu a//b và b//c thì...a//c.... (từ vuông góc đến song song)
TT
2
14 tháng 3 2023
Vì góc B>goc C
và AC,AB lần lượt là cạnh đối diện của góc B và góc C
nên AC>AB
14 tháng 3 2023
Từ giả thiết, có \(\widehat {B} > \widehat {C}\)
Theo định lý `2` của quan hệ giữa góc đối diện và cạnh đối diện `-> AC > AB`
20 tháng 11 2021
a. Vì m⊥t và n⊥t nên m//n
b. Vì m//n nên \(\widehat{D}=\widehat{C_3}=75^0\) (so le trong)
Ta có \(\widehat{C_4}=180^0-\widehat{C_3}=105^0\) (kề bù)
20 tháng 11 2021
a) vì \(m\perp t\) mà \(n\perp t\)
=> m//n
b) vì m//n
=>\(D+C_4=180^O\\C_4 =180^O-D=105^O\)
D=C3=75o
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
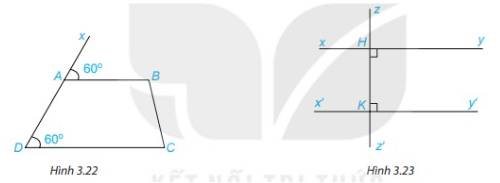
1. Vì \(\widehat {BAx} = \widehat {CDA}( = 60^\circ )\)
Mà 2 góc này ở vị trí đồng vị
\( \Rightarrow \) AB//CD (Dấu hiệu nhận biết hai đường thẳng song song)
2. Ta có: \(\widehat {zKy'} + \widehat {y'Kz'} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow 90^\circ + \widehat {y'Kz'} = 180^\circ \\ \Rightarrow \widehat {y'Kz'} = 180^\circ - 90^\circ = 90^\circ \end{array}\)
Vì \(\widehat {yHz'} = \widehat {y'Kz'}\)
Mà 2 góc này ở vị trí đồng vị
\( \Rightarrow \) xy // x’y’ (Dấu hiệu nhận biết hai đường thẳng song song)
Chú ý:
2 đường thẳng cùng vuông góc với 1 đường thẳng thứ ba thì 2 đường thẳng đó song song.
24 tháng 9 2023
Bạn ơi, đây là CH bạn ý đăng ở Hoc24. Còn CH mà bạn giải được bạn í đăng ở web Olm, chứ không phải bạn kia cố tình đăng 2 lần đâu nhé!
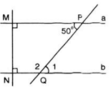
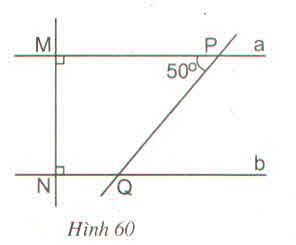
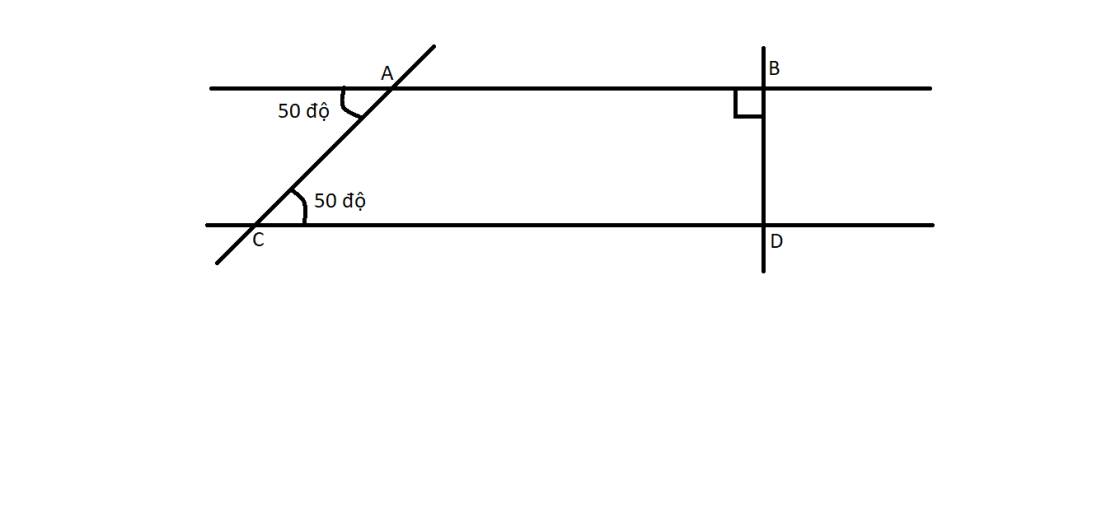
Theo hình vẽ ta có: a ⊥ MN, b ⊥ MN ⇒ a // b (quan hệ từ vuông góc đến song song)