
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo hình vẽ ta có: a ⊥ MN, b ⊥ MN ⇒ a // b (quan hệ từ vuông góc đến song song)

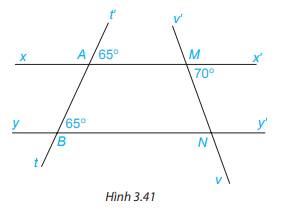
a) Vì \(\widehat {t'AM} = \widehat {ABN}( = 65^\circ )\), mà 2 góc này ở vị trí đồng vị nên xx’//yy’ ( Dấu hiệu nhận biết 2 đường thẳng song song.)
b) Vì xx’//yy’ nên \(\widehat {x'MN} = \widehat {MNB}\)( 2 góc so le trong), mà \(\widehat {x'MN} = 70^\circ \Rightarrow \widehat {MNB} = 70^\circ \)

a. Vì m⊥t và n⊥t nên m//n
b. Vì m//n nên \(\widehat{D}=\widehat{C_3}=75^0\) (so le trong)
Ta có \(\widehat{C_4}=180^0-\widehat{C_3}=105^0\) (kề bù)
a) vì \(m\perp t\) mà \(n\perp t\)
=> m//n
b) vì m//n
=>\(D+C_4=180^O\\C_4 =180^O-D=105^O\)
D=C3=75o

a, Ta có:
AB \(\perp\) a
AB \(\perp\) b
\(\Rightarrow\)a // b
b, Ta có: a // b( câu a)
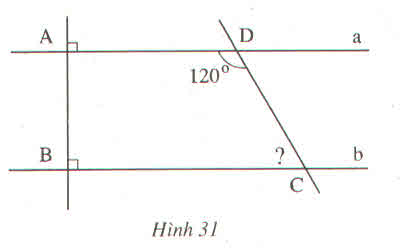
hai góc ADC và DCB là hai góc trong cùng phía
\(\Rightarrow\)DCB = 180\(^0\) - ADC(tính chất hai đường thẳng song song)
\(\Rightarrow\) DCB = 180\(^0\)-120\(^0\) = 60\(^0\)
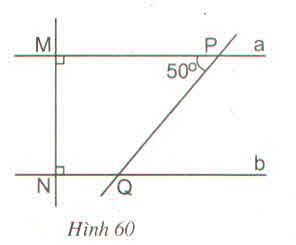

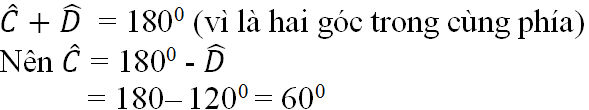
a) Hai đường thẳng a và b cùng vuông góc với đường thẳng MN nên a // b.
b) Ta có góc MPQ = góc Q1 = 50o (so le trong vì a // b)
mà góc Q1 + Q2 = 180o (kề bù)
=> Q2 = 180o - 50o = 130o
Vậy góc NQP = 130o.
Kí hiệu như hình vẽ.
Ta có tứ giác ISTM nội tiếp đường tròn nên:
ˆS1S1^ + ˆMM^ = 180o
Mà ˆM1M1^ + ˆM3M3^ = 180o (kề bù)
nên suy ra ˆS1S1^ = ˆM3M3^ (1)
Tương tự từ các tứ giác nội tiếp IMPN và INQS ta được
ˆM3M3^ = ˆN4N4^ (2)
ˆN4N4^ = ˆR2R2^ (3)
Từ (1), (2), (3) suy ra
Do đó QR // ST