Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét hình thang ADCB có
Q,P lần lượt là trung điểm của AB,DC
=>QP là đường trung bình của hình thang ADCB
=>QP//AD//BC và \(QP=\dfrac{AD+BC}{2}=\dfrac{\dfrac{BC}{2}+BC}{2}=\dfrac{3}{4}BC\)
Ta có: M là trung điểm của BC
=>\(BM=MC=\dfrac{BC}{2}\)
Ta có: N là trung điểm của MC
=>\(MN=NC=\dfrac{MC}{2}=\dfrac{BC}{4}\)
BM+MN=BN
=>\(BN=\dfrac{1}{4}BC+\dfrac{1}{2}BC=\dfrac{3}{4}BC\)
=>QP=BN
Ta có: QP//BN
QP=BN
Do đó: \(\overrightarrow{QP}=\overrightarrow{BN}\)
=>Điểm E trùng với điểm P

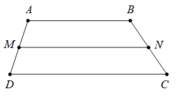
Vì M; N lần lượt là trung điểm của AD; BC
M A → + M D → = 0 → B N → + C N → = 0 → .
Dựa vào đáp án, ta có nhận xét sau:
A đúng, vì :
M D → + C N → + D C → = M N → = M D → + D C → + C N → = M C → + C N → = M N → .
B đúng, vì A B → − M D → + B N → = A B → + B N → − M D → = A N → − A M → = M N → .
C đúng, vì M N → = M A → + A B → + B N → và M N → = M D → + D C → + C N → .
Suy ra
2 M N → = M A → + M D → + A B → + D C → + B N → + C N → = 0 → + A B → + D C → + 0 → = A B → + D C →
⇒ M N → = 1 2 A D → + B C → .
D sai, vì theo phân tích ở đáp án C.
Chọn D.

Xét ΔADB có
\(cosA=\dfrac{AB^2+AD^2-DB^2}{2\cdot AB\cdot AD}\)
=>\(\dfrac{a^2+9a^2-DB^2}{2\cdot a\cdot3a}=\dfrac{1}{2}\)
=>\(10a^2-DB^2=3a^2\)
=>\(DB=a\sqrt{7}\)
Xét ΔABD có
\(cosABD=\dfrac{BA^2+BD^2-AD^2}{2\cdot BA\cdot BD}\)
\(=\dfrac{9a^2+7a^2-a^2}{2\cdot3a\cdot a\sqrt{7}}=\dfrac{15a^2}{6a^2\cdot\sqrt{7}}=\dfrac{15}{6\sqrt{7}}=\dfrac{5}{2\sqrt{7}}\)
=>\(cosCDB=\dfrac{5}{2\sqrt{7}}\)(do \(\widehat{ABD}=\widehat{CDB}\) vì AB//CD)
Xét ΔCDB có \(cosCDB=\dfrac{DB^2+DC^2-BC^2}{2\cdot DB\cdot DC}\)
=>\(\dfrac{5}{2\sqrt{7}}=\dfrac{7a^2+a^2-BC^2}{2\cdot a\sqrt{7}\cdot a}\)
=>\(\dfrac{8a^2-BC^2}{2a^2\sqrt{7}}=\dfrac{5}{2\sqrt{7}}\)
=>\(\dfrac{8a^2-BC^2}{a^2}=5\)
=>\(8a^2-BC^2=5a^2\)
=>\(BC^2=3a^2\)
=>\(BC=a\sqrt{3}\)

Gọi \(\overrightarrow{n}=\left(a,b\right)\) là vectơ pháp tuyến của CD (\(a^2+b^2\ne0\)
Ta có phương trình CD : \(ax+by+a+b=0\)
\(S_{BCD}=S_{ACD}=8\Rightarrow d\left(A;CD\right)=\frac{2.S}{CD}=2\Rightarrow d\left(M.CD\right)=1\)
\(\Rightarrow\frac{\left|2a-b\right|}{\sqrt{a^2+b^2}}=1\Leftrightarrow3a^2-4ab=0\)\(\rightarrow\begin{cases}a=0;b=1\\a=4;b=3\end{cases}\)\(\rightarrow\begin{cases}CD:y+1=0\\CD:4x+3y+7=0\end{cases}\)
Với \(CD:y+1=0\rightarrow D\left(d;-1\right);CD^2=4.AB^2=64\Leftrightarrow\begin{cases}d=7\\d=-9:L\end{cases}\)
\(D\left(7;-1\right);\overrightarrow{AB}=\frac{1}{2}\overrightarrow{DC}=\left(-4;0\right)\rightarrow B\left(-9;-3\right)\)
Với \(CD:4x+3y+7=0\rightarrow D\left(d;\frac{-4d-7}{3}\right)\rightarrow CD^2=\frac{25\left(d+1\right)^2}{9}=64\) (loại)
