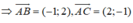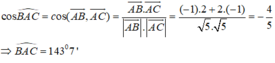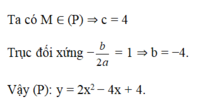Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A=[1;5]
B=(-3;2) hợp (3,7)
=> A giao B=[1;2) hợp với (3;5]

a) [-3;1) ∪ (0;4] = [-3; 4]
b) (0; 2] ∪ [-1;1) = [-1; 2]
c) (-2; 15) ∪ (3; +∞) = (-2; +∞)
d) (-1; 4/3) ∪ [-1; 2)=(-1; 2)
e) (-∞; 1) ∪ (-2; +∞)= (-∞; +∞)
a) [-3;1) ∪ (0;4];
b) (0; 2] ∪ [-1;1);
c) (-2; 15) ∪ (3; +∞);
d) (-1;4/3) ∪ [-1; 2)
e) (-∞; 1) ∪ (-2; +∞).

B.5 X giao Y = [ -3;1) giao (0;4) =(0;1)
X hợp Y = [-3;1) hợp (0;4) = [ -3;4)

\(AB=\sqrt{\left(1-3\right)^2+\left(5+4\right)^2}=\sqrt{85}\)
\(BC=\sqrt{\left(3-1\right)^2+\left(1-5\right)^2}=2\sqrt{5}\)
\(CA=\sqrt{\left(3-3\right)^2+\left(-4-1\right)^2}=5\)
\(p=\frac{\sqrt{85}+2\sqrt{5}+5}{2}\)
\(p-AB=\frac{2\sqrt{5}+5-\sqrt{85}}{2};p-BC=\frac{\sqrt{85}+5-2\sqrt{5}}{2};p-CA=\frac{\sqrt{85}+2\sqrt{5}-5}{2}\)
\(\Rightarrow S_{ABC}=\sqrt{p\left(p-AB\right)\left(p-BC\right)\left(p-CA\right)}=...\)

\(\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{2}{2a}=1\\-\dfrac{2^2-4ac}{4a}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-1\\4+4c=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-1\\c=4\end{matrix}\right.\)

Theo đề, ta có:
\(\left\{{}\begin{matrix}\dfrac{-2}{2a}=-1\\-\dfrac{4-4ac}{4a}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\4-4c=-20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\c=6\end{matrix}\right.\)

\(\overrightarrow{BC}=\left(-5;7\right)\Rightarrow\) đường thẳng BC nhận (7;5) là 1 vtpt
Phương trình tổng quát của BC (đi qua B) có dạng:
\(7\left(x-6\right)+5\left(y+2\right)=0\Leftrightarrow7x+5y-32=0\)
b.
Gọi H là chân đường cao ứng với BC
\(\Rightarrow AH=d\left(A;BC\right)=\dfrac{\left|7.0+5.4-32\right|}{\sqrt{7^2+5^2}}=\dfrac{6\sqrt{74}}{37}\)
\(BC=\sqrt{\left(-5\right)^2+7^2}=\sqrt{74}\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=6\)

a \(R=d_{\left(I;\Delta\right)}=\dfrac{\left|2\cdot\left(-1\right)-2+3\right|}{\sqrt{2^2+\left(-1\right)^2}}=\dfrac{\sqrt{5}}{5}\)
\(\Rightarrow\)PT đường tròn là: (x+1)2 + (y-2)2=\(\dfrac{1}{5}\)
b tâm I là trung điểm AB \(\Rightarrow\)I (-1;3)
\(R=\dfrac{1}{2}AB=\dfrac{1}{2}\cdot\sqrt{\left(1+3\right)^2+\left(5-1\right)^2}=2\sqrt{2}\)
\(\Rightarrow\) PT đường tròn là: (x+1)2 + (y-3)2=8