
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: (x+2)(x-3)>0
nên x+2;x-3 cùng dấu
=>x>3 hoặc x<-2
b: (x-1)(x+4)<=0
nên x-1 và x+4 khác dấu
=>-4<=x<=1

Ta có: x=2
nên x-1=1
Ta có: \(B=\left(x+1\right)\left(x^7-x^6+x^5-x^4+x^3-x^2+x-1\right)\)
\(=\left(x+1\right)\left[x^6\left(x-1\right)+x^4\left(x-1\right)+x^2\left(x-1\right)+\left(x-1\right)\right]\)
\(=\left(x+1\right)\left(x^6+x^4+x^2+1\right)\)
\(=\left(x+1\right)\left(x+1\right)\left(x^4+1\right)\)
\(=\left(2^4+1\right)\left(2+1\right)^2=17\cdot9=153\)

a)Ta có: \(\dfrac{x+3}{x+1}+\dfrac{1}{3}\ge0\)
\(\Leftrightarrow\dfrac{3x+9+x+1}{3\left(x+1\right)}\ge0\)
\(\Leftrightarrow\dfrac{4x+10}{3x+3}\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1>0\\4x+10\le0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>-1\\x\le-\dfrac{5}{2}\end{matrix}\right.\)
b) Ta có: \(\dfrac{x+2}{x+3}+\dfrac{1}{3}\le0\)
\(\Leftrightarrow\dfrac{3x+6+x+3}{3\left(x+3\right)}\le0\)
\(\Leftrightarrow\dfrac{4x+9}{3x+9}\le0\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x+9>0\\4x+9\le0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>-3\\x\le-\dfrac{9}{4}\end{matrix}\right.\Leftrightarrow-3< x\le-\dfrac{9}{4}\)
a)\(\dfrac{x+3}{x+1}\ge-\dfrac{1}{3}\left(x\ne-1\right)\)
\(\Leftrightarrow\dfrac{x+3}{x+1}+\dfrac{1}{3}\ge0\)
\(\Leftrightarrow\dfrac{3x+9+x+1}{3x+3}\ge0\)
\(\Leftrightarrow\dfrac{4x+10}{3x+3}\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}4x+10\ge0\\3x+3>0\end{matrix}\right.\\\left\{{}\begin{matrix}4x+10\le0\\3x+3< 0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge-\dfrac{5}{2}\\x>-1\end{matrix}\right.\\\left\{{}\begin{matrix}x\le\dfrac{-5}{2}\\x< -1\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x>-1\\x\le\dfrac{-5}{2}\end{matrix}\right.\)
b) \(\dfrac{x+2}{x+3}\le-\dfrac{1}{3}\left(x\ne-3\right)\)
\(\dfrac{x+2}{x+3}+\dfrac{1}{3}\le0\)
\(\Leftrightarrow\dfrac{3x+6+x+3}{3x+9}\le0\)
\(\Leftrightarrow\dfrac{4x+9}{3x+9}\le0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}4x+9\ge0\\3x+9< 0\end{matrix}\right.\\\left\{{}\begin{matrix}4x+9\le0\\3x+9>0\end{matrix}\right.\end{matrix}\right.\)
\(\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge-\dfrac{9}{4}\\x< -3\end{matrix}\right.\\\left\{{}\begin{matrix}x\le-\dfrac{9}{4}\\x>-3\end{matrix}\right.\end{matrix}\right.\)
TH1: loại
TH2: TM
Vậy no của BPT là :\(-\dfrac{9}{4}\ge x>-3\)
chúc bạn học tốt

\(x^5+x^4+x+1=0\)
\(\Leftrightarrow x^4\left(x+1\right)+\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^4+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x^4+1=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^4=-1\end{matrix}\right.\)
\(\Rightarrow x=-1\) (do \(x^4\ge0\forall x\))
Vậy x = -1
\(x^5+x^4+x+1=0\)
\(\Leftrightarrow\left(x^5+x^4\right)+\left(x+1\right)=0\)
\(\Leftrightarrow x^4\left(x+1\right)+\left(x+1\right)=0\)
\(\Leftrightarrow\left(x^4+1\right)\left(x+1\right)=0\) (Mà: \(x^4+1\ge1>0\forall x\))
\(\Leftrightarrow x+1=0\)
\(\Leftrightarrow x=-1\)

a. $6x^2-11x=x(6x-11)$
b. $x^7+x^5+1=(x^7-x)+(x^5-x^2)+x+x^2+1$
$=x(x^6-1)+x^2(x^3-1)+(x^2+x+1)$
$=x(x^3-1)(x^3+1)+x^2(x^3-1)+(x^2+x+1)$
$=(x^3-1)(x^4+x+x^2)+(x^2+x+1)$
$=(x-1)(x^2+x+1)(x^4+x^2+x)+(x^2+x+1)$
$=(x^2+x+1)[(x-1)(x^4+x^2+x)+1]$
$=(x^2+x+1)(x^5-x^4+x^3-x+1)$
c.
$x^8+x^4+1=(x^4)^2+2.x^4+1-x^4$
$=(x^4+1)^2-(x^2)^2$
$=(x^4+1-x^2)(x^4+1+x^2)$
$=(x^4+1-x^2)(x^4+2x^2+1-x^2)$
$=(x^4-x^2+1)[(x^2+1)^2-x^2]$
$=(x^4-x^2+1)(x^2+1-x)(x^2+1+x)$
d.
$x^3-5x+8-4=x^3-5x+4$
$=x^3-x^2+x^2-x-(4x-4)$
$=x^2(x-1)+x(x-1)-4(x-1)=(x-1)(x^2+x-4)$
e.
$x^5+x^4+1=(x^5-x^2)+(x^4-x)+x^2+x+1$
$=x^2(x^3-1)+x(x^3-1)+x^2+x+1$
$=(x^3-1)(x^2+x)+(x^2+x+1)$
$=(x-1)(x^2+x+1)(x^2+x)+(x^2+x+1)$
$=(x^2+x+1)[(x-1)(x^2+x)+1]$
$=(x^2+x+1)(x^3-x+1)$


b) \(25-x^2+14xy-49y^2\)
\(=25-\left(x^2-14xy+49y^2\right)\)
\(=25-\left[x^2-2\cdot7y\cdot x+\left(7y\right)^2\right]\)
\(=25-\left(x-7y\right)^2\)
\(=5^2-\left(x-7y\right)^2\)
\(=\left[5-\left(x-7y\right)\right]\left[5+\left(x-7y\right)\right]\)
\(=\left(5-x+7y\right)\left(5+x-7y\right)\)
c) \(x^5+x^4+1\)
\(=x^5+x^4+1+x^3-x^3\)
\(=\left(x^5+x^4+x^3\right)+\left(1-x^3\right)\)
\(=x^3\left(x^2+x+1\right)+\left(1-x\right)\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left[x^3+\left(1-x\right)\right]\)
\(=\left(x^2+x+1\right)\left(x^3+1-x\right)\)
b: 25-x^2+14xy-49y^2
=25-(x-7y)^2
=(5-x+7y)(5+x-7y)
c: =x^5+x^4+x^3+1-x^3
=x^3(x^2+x+1)+(1-x)(x^2+x+1)
=(x^2+x+1)(x^3+1-x)

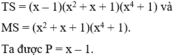
phân tích à :
x^5 + 1
= x^5 + x^4 - x^4 - x^3 + x^3 + x^2 - x^2 + 1
= x^4(x+1) - x^3(x+1) + x^2(x + 1) + (1-x)(1+x)
= (x+1)(x^4 - x^3 + x^2 + 1 - x)
x^4 + 1
= x^4 + 2x^2 + 1 - 2x^2
= (x^2 + 1)^2 - 2x^2
= (x^2 + 1 - x√2)(x^2 + 1 + x√2)