K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 3 2022
\(\Leftrightarrow x^3-2x^2-6x^2+12x+9x-18=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2-6x+9\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)^2=0\)
=>x=2 hoặc x=3
17 tháng 3 2020
x3 - 8.x2 + 21.x - 18 = 0
<=> x3 - 2.x2 -6.x2 +12.x + 9.x -18 = 0
<=> x2 . (x-2 ) - 6.x . ( x - 2 ) + 9.(x - 2 ) =0
<=> (x-2 ) . ( x2 - 6.x + 9 ) = 0
<=> (x-2 ) . ( x-3 )2 = 0
<=> \(\orbr{\begin{cases}x-2=0\\\left(x-3\right)^2=0\end{cases}}\)
<=> \(\orbr{\begin{cases}x=2\\x=3\end{cases}}\)
Vậy phương trình trên có tập nghiệm { 2;3 }
DE
17 tháng 3 2020
\(x^3-8x^2+21x-18=0\)
\(\Leftrightarrow x^3-2x^2-6x^2+12x+9x-18=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2-6x+9\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)^2=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x-3=0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=2\\x=3\end{cases}}\)
17 tháng 3 2020
\(x^3-8x^2+21x-18=0\)
\(\left(x^2-6x+9\right)\left(x-2\right)=0\)
\(\left(x-3\right)^2\left(x-2\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-3=0\\x-2=0\end{cases}\Rightarrow\orbr{\begin{cases}x=3\\x=2\end{cases}}}\)
MD
2
14 tháng 3 2022
g: =>(x-1)(x-2)=0
=>x=1 hoặc x=2
i: \(\Leftrightarrow x^4-x^3+x^3-x^2+2x^2-2x+8x-8=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^3+x^2+2x+8\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x^2-x+4\right)=0\)
=>x=1 hoặc x=-2
M0
2
14 tháng 3 2022
g: \(x^2-3x+2=0\)
=>(x-1)(x-2)=0
=>x=1 hoặc x=2
i: \(x^4+x^2+6x-8=0\)
\(\Leftrightarrow x^4-x^3+x^3-x^2+2x^2-2x+8x-8=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^3+x^2+2x+8\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left[\left(x+2\right)\left(x^2-2x+4\right)+x\left(x+2\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x^2-x+4\right)=0\)
=>x=1 hoặc x=-2
TH
4
5 tháng 2 2020
(x^3-9x^2+27x-27)+(x^2-6x+9)=0
(x-3)^3+(x-3)^2=0
(x-3)^2(x-2)=0
<=>x-3=0 hoặc x-2=0
<=>x=3 hoặc x=2
BB
0
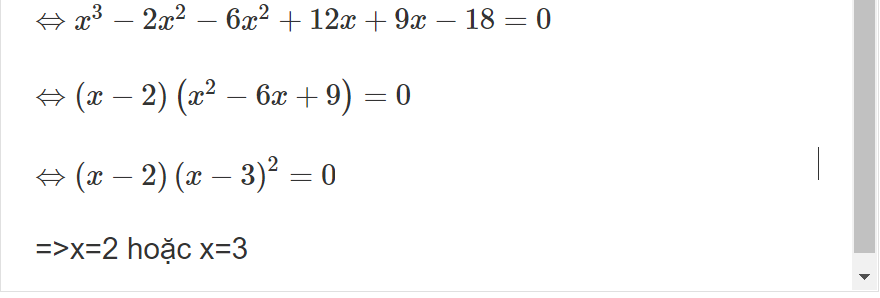
\(x^3-8x^2+21x-18=0\)
\(\Leftrightarrow x^3-2x^2-6x^2+12x+9x-18=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2-6x+9\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)^2=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=2\\x=3\end{cases}}\)
Kham khảo