
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


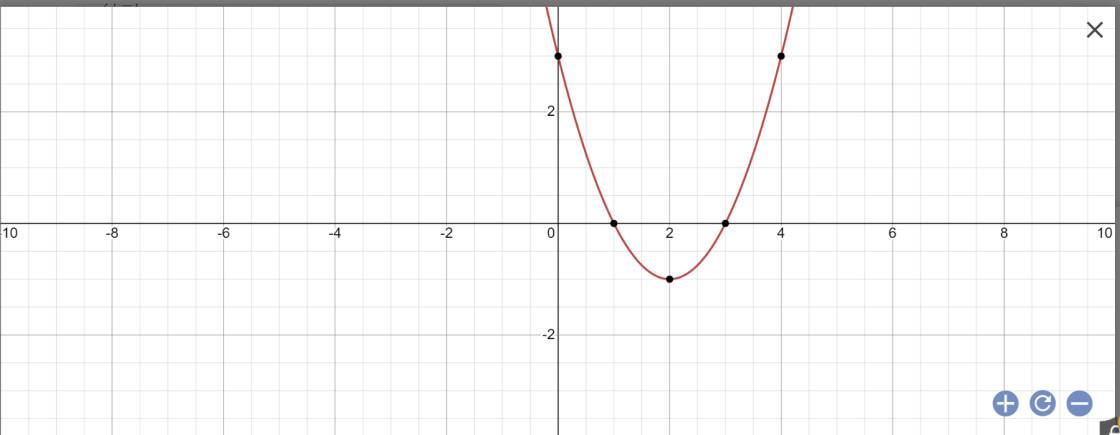
a)\(y=x^2-4x+3=\left(x-3\right)\left(x-1\right)\)
b)\(y=x^2+4x+3=\left(x+1\right)\left(x+3\right)\)
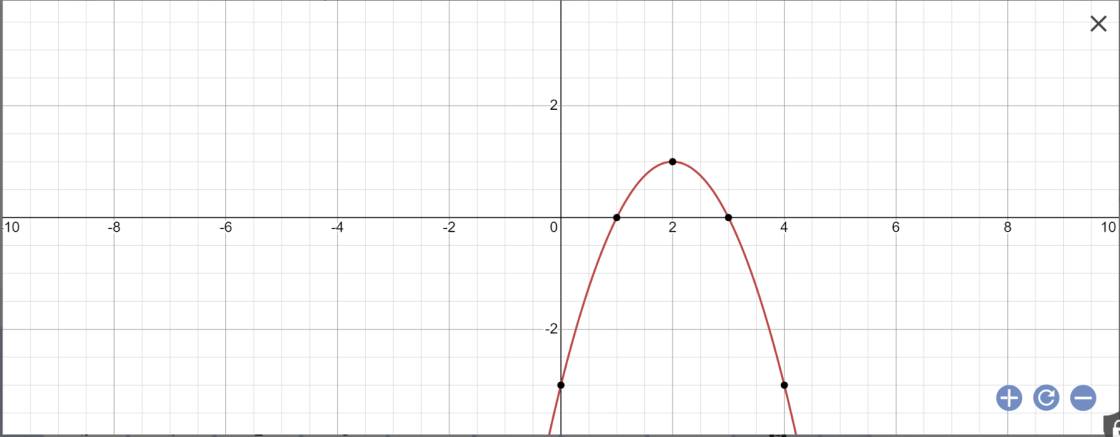
c)\(y=-x^2+4x-3=\left(x-3\right)\left(x-1\right)\)
d)\(y=-x^2-4x-3=\left(x+1\right)\left(x+3\right)\)

Phương trình ⇔ 4 x − 17 ≥ 0 x 2 − 4 x − 5 = 4 x − 17 2
⇔ x ≥ 17 4 x 2 − 5 x − 5 2 = 4 x − 17 2
⇔ x ≥ 17 4 ( x 2 − 8 x + 12 ) ( x 2 − 22 ) = 0 ⇔ x ≥ 17 4 x 2 − 8 x + 12 = 0 x 2 − 22 = 0
⇔ x ≥ 17 4 x = 2 ∨ x = 6 x = ± 22 ⇔ x = 6 x = 22 ⇒ P = 22 2 + 6 = 28
Đáp án cần chọn là: C

a, \(\left(x-3\right)\left(x^2+x-20\right)\ge0\)
\(\Leftrightarrow\) \(\left(x-3\right)\left(x-4\right)\left(x+5\right)\ge0\)
+) \(x-3=0\Leftrightarrow x=3\); \(x-4=0\Leftrightarrow x=4\); \(x+5=0\Leftrightarrow x=-5\)
+) Lập trục xét dấu f(x) (Bạn tự kẻ trục nha)
\(\Rightarrow\) Bpt có tập nghiệm S = \(\left[-5;3\right]\cup\) [4; \(+\infty\))
b, \(\dfrac{x^2-4x-5}{2x+4}\ge0\)
\(\Leftrightarrow\) \(\dfrac{\left(x-5\right)\left(x+1\right)}{2x+4}\ge0\)
+) \(x-5=0\Leftrightarrow x=5\); \(x+1=0\Leftrightarrow x=-1\); \(2x+4=0\Leftrightarrow x=-2\)
+) Lập trục xét dấu f(x)
\(\Rightarrow\) Bpt có tập nghiệm S = (-2; -1] \(\cup\) [5; \(+\infty\))
c, \(\dfrac{-1}{x^2-6x+8}\le1\)
\(\Leftrightarrow\) \(\dfrac{\left(x-3\right)^2}{\left(x-4\right)\left(x-2\right)}\ge0\)
+) \(x-3=0\Leftrightarrow x=3\); \(x-4=0\Leftrightarrow x=4\); \(x-2=0\Leftrightarrow x=2\)
+) Lập trục xét dấu f(x)
\(\Rightarrow\) Bpt có tập nghiệm S = (\(-\infty\); 2) \(\cup\) (4; \(+\infty\))
Chúc bn học tốt!

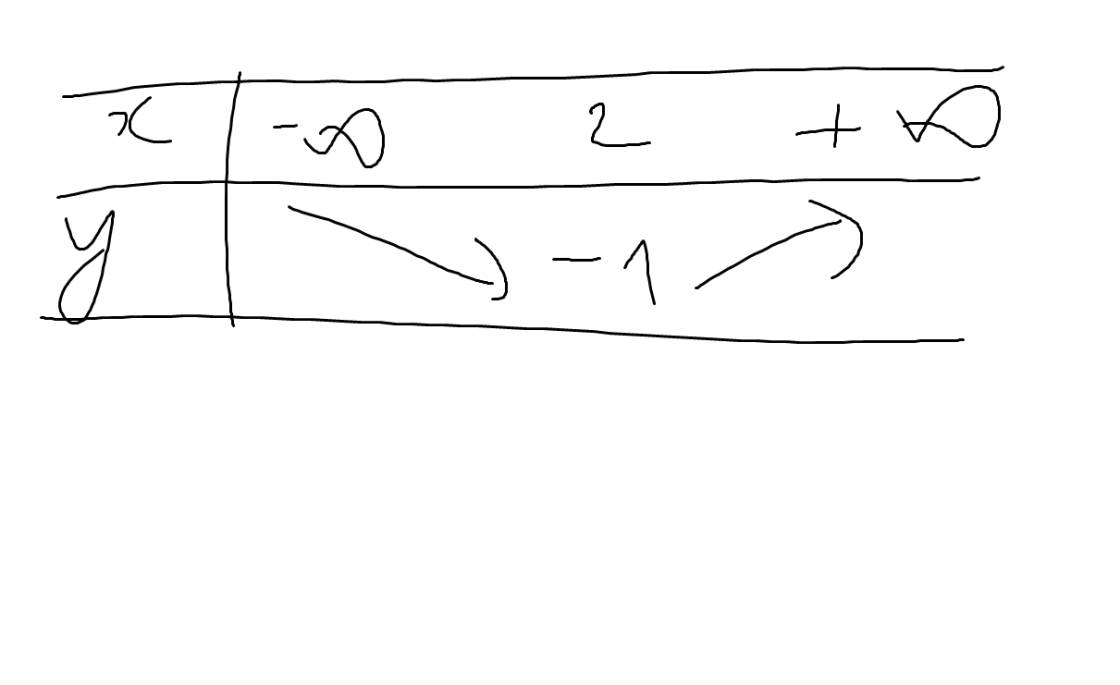
b: Tọa độ đỉnh của (P): y=x2-4x+3 là:
\(\left\{{}\begin{matrix}x=\dfrac{-b}{2a}=\dfrac{-\left(-4\right)}{2}=\dfrac{4}{2}=2\\y=-\dfrac{b^2-4ac}{4a}=-\dfrac{\left(-4\right)^2-4\cdot1\cdot3}{4}=-\dfrac{16-12}{4}=-1\end{matrix}\right.\)
Bảng biến thiên:
Vẽ đồ thị hàm số:
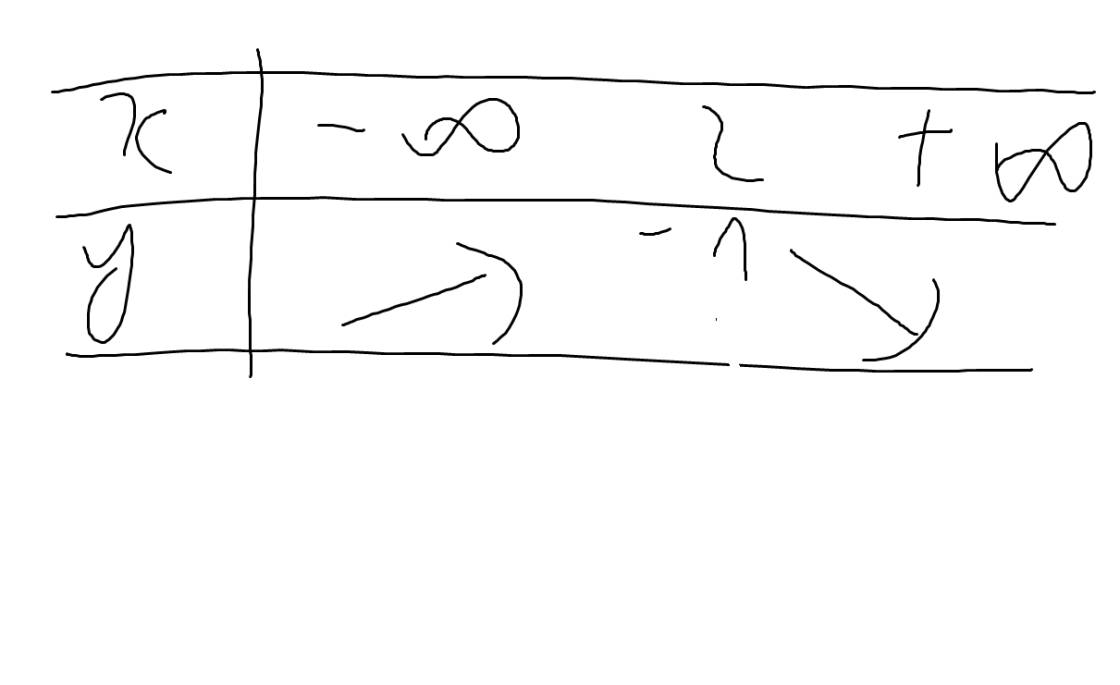
e: Tọa độ đỉnh của (P): y=-x2+4x-3 là:
\(\left\{{}\begin{matrix}x=\dfrac{-b}{2a}=\dfrac{-4}{2\cdot\left(-1\right)}=\dfrac{4}{2}=2\\y=-\dfrac{b^2-4ac}{4a}=-\dfrac{4^2-4\cdot\left(-1\right)\cdot\left(-3\right)}{4\cdot\left(-1\right)}=1\end{matrix}\right.\)
Bảng biến thiên:
vẽ đồ thị hàm số:

a) x2-4x+3=0
có Δ' = b'2-ac= 4-3=1 >0
nên phương trình có 2 nghiệm phân biệt: x1= 3; x2= 1
b) x2 -4=0
⇔ x2=4
⇔\(\left[{}\begin{matrix}x=-2\\x=2\end{matrix}\right.\)
c)x2+4x=0
⇔x (x+4)=0
⇔\(\left[{}\begin{matrix}x=0\\x+4=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)

Bạn cần viết đề bài bằng công thức toán để được hỗ trợ tốt hơn.

x2+4x+2m+1=0 \(\Leftrightarrow\) x2+4x+3=-2m+2.
Phương trình đã cho có tối đa một nghiệm âm, xảy ra khi -2m+2>3.
Vậy không có giá trị nào của m thỏa yêu cầu đề bài.
Xin lỗi! Mình bất cẩn, bạn kiểm tra lại đồ thị giúp mình, bạn nhầm đồ thị rồi!
Giải:
x2+4x+2m+1=0 ⇔ x2+4x+3=-2m+2.
f(0)=3.
Ycđb \(\Leftrightarrow\) -1<-2m+2<3 \(\Rightarrow\) -1/2<m<3/2.

Bạn kiểm tra đồ thị giúp mình, nhầm đồ thị rồi!
x2+4x+m-3=0 \(\Leftrightarrow\) x2+4x+3=6-m.
f(-3)=0.
Ycđb \(\Leftrightarrow\) 6-m>0 \(\Rightarrow\) m<6.

