K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2 tháng 11 2023
`#3107.101107`
\(\left(3^x-81\right)\left(x^2+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}3^x-81=0\\x^2+1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}3^x=81\\x^2=-1\left(\text{vô lý}\right)\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}3^x=3^3\\x\in\varnothing\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\\x\in\varnothing\end{matrix}\right.\)
Vậy, `x = 3.`
b) 3x +x2 = 0 c) (x-1)(x-3) < 0
6 tháng 1 2022
\(b,3x+x^2=0\\ \Rightarrow x\left(3+x\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=-3\end{matrix}\right.\\ c,\left(x-1\right)\left(x-3\right)< 0\\ \Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-1< 0\\x-3>0\end{matrix}\right.\\\left\{{}\begin{matrix}x-1>0\\x-3< 0\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x< 1\\x>3\left(vô.lí\right)\end{matrix}\right.\\\left\{{}\begin{matrix}x>1\\x< 3\end{matrix}\right.\end{matrix}\right.\)
Vậy 1<x<3
PT
1
TT
0
10 tháng 9 2017
Tham khảo nhé :
\(\left|x-2\right|-3x\left|+\right|x-1\left|x-3\right|=0\)
\(\Leftrightarrow\left|x-2\right|-3=0\)hoặc \(5+\left|x\right|=0\)
Xét \(\left|x-2\right|-3=0\Leftrightarrow\left|x-2\right|=3\)
\(\Rightarrow x-2=\pm3\)
Với: \(x-2=3\Rightarrow x=5\)
Với: \(x-2=-3\Rightarrow x=-1\)
Vậy:..
6T
3
12 tháng 3 2023
`x^2 - 3x = 0`
`<=> x(x-3) =0 `
`<=> x = 0` hoặc `x = 3`.
`-> C`
NK
1
2 tháng 7 2020
2. \(A\left(x\right)=x^2+3x-4=x^2+4x-x-4=x\left(x+4\right)-\left(x+4\right)=\left(x+4\right)\left(x-1\right)\)
A(x) >0 => (x+4)(x-1) cùng dấu
TH1: x+4; x-1 cùng âm \(\hept{\begin{cases}x+4< 0\\x-1< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x< -4\\x< 1\end{cases}\Leftrightarrow}x< -4}\)
TH2: x+4;x-1 cùng dương \(\hept{\begin{cases}x+4>0\\x-1>0\end{cases}\Leftrightarrow\hept{\begin{cases}x>-4\\x>1\end{cases}\Leftrightarrow}x>1}\)
3. \(A\left(x\right)=\left(x+4\right)\left(x-1\right)\)
A(x) <0 => \(\orbr{\begin{cases}x+4< 0\\x-1< 0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x< -4\\x< 1\end{cases}}\)
Vậy x<-4 hoặc x<1 thì A(x)<0
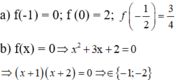
x2+3x=0
=> x.(x+3)=0
=> x=0
x+3=0 => x=0-3 =>x=-3
Vậy x=-3;0
k nha