K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 7 2021
Bài 10:
a) (x+2)2 -x(x+3) + 5x = -20
=> x2 + 4x + 4 - x2 - 3x + 5x = -20
=> 6x = -20 + (-4)
=> 6x = -24
=> x = -4
b) 5x3-10x2+5x=0
=>5x(x2-2x+1)=0
=>5x(x-1)2 =0
=> 5x=0 hoặc (x-1)2=0
=>x=0 hoặc x=1
c) (x2 - 1)3 - (x4 + x2 + 1)(x2 - 1) = 0
=> (x2 - 1)[(x2 - 1)2 - (x4 + x2 + 1)] = 0
<=> (x2 - 1)(x4 - 2x2 + 1 - x4 - x2 - 1) = 0
<=> (x2 - 1)(-3x2) = 0
<=> (x2 - 1)=0 hoặc (-3x2) =0
<=> x2=1 hoặc x2=0
<=> x=−1;1 hoặc x=0
d)
(x+1)3−(x−1)3−6(x−1)2=-19
⇔x3+3x2+3x+1−(x3−3x2+3x−1)−6(x2−2x+1)+19=0
⇔x3+3x2+3x+1−x3+3x2−3x+1−6x2+12x−6+19=0
⇔12x+13=0⇔12x+13=0
⇔12x=-13
⇔x=-23/12
Học tốt nhé:333
3 tháng 8 2023
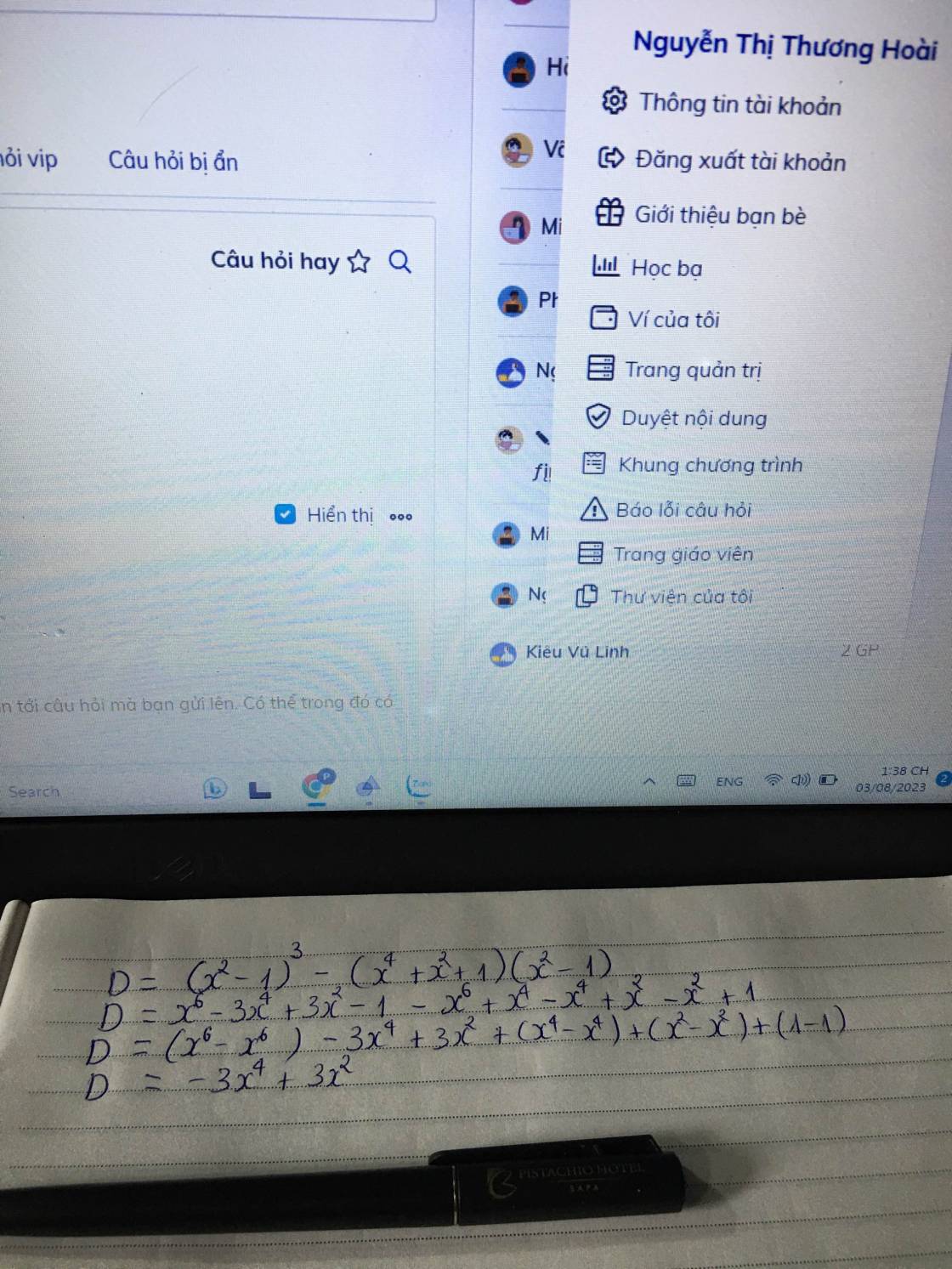
\(D=\left(x^2-1\right)^3-\left(x^4+x^2+1\right)\left(x^2-1\right)\)
\(\Rightarrow D=x^6-3x^4+3x^2-1-\left(x^6-1\right)\)
\(\Rightarrow D=-3x^4+3x^2=3x^2\left(1-x^2\right)\)
10 tháng 9 2021
\(a,=x+x^2-x^3+x^4-x^5+1+x-x^2+x^3-x^4-x-x^2+x^3-x^4+x^5+1+x-x^2+x^3-x^4\\ =2x-2x^2+2x^3-2x^4\)
DT
18 tháng 2 2022
a, \(\Leftrightarrow\left(9x^2-4\right)\left(x+1\right)-\left(3x+2\right)\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(\left(9x^2-4\right)-\left(\left(3x+2\right)\left(x-1\right)\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-\left(3x^2-x-2\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-3x^2+x+2\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x^2+x-2\right)=0\)
\(\Leftrightarrow\left(x+1\right)=0;3x^2+x-2=0\)
=> x=-1
với \(3x^2+x-2=0\)
ta sử dụng công thức bậc 2 suy ra : \(x=\dfrac{2}{3};x=-1\)
Vậy ghiệm của pt trên \(S\in\left\{-1;\dfrac{2}{3}\right\}\)
18 tháng 2 2022
b: \(\Leftrightarrow x^2-2x+1-1+x^2=x+3-x^2-3x\)
\(\Leftrightarrow2x^2-2x=-x^2-2x+3\)
\(\Leftrightarrow3x^2=3\)
hay \(x\in\left\{1;-1\right\}\)
c: \(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x+2\right)\left(x-3\right)-\left(x-1\right)\left(x-2\right)\left(x+2\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left[\left(x+1\right)\left(x-3\right)-\left(x-2\right)\left(x+5\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x^2-2x-3-x^2-3x+10\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(-5x+7\right)=0\)
hay \(x\in\left\{1;-2;\dfrac{7}{5}\right\}\)
\(\left(x^2-1\right)^3-\left(x^4+x^2+1\right)\left(x^2-1\right)=0\)
\(\Leftrightarrow x^5-3x^4+3x^2-1-\left(x^6-x^4+x^4-x^2+x^2-1\right)=0\)
\(\Leftrightarrow x^5-3x^4+3x^2-x^6=0\)
\(\Leftrightarrow x^5\left(1-x\right)-3x^2\left(x^2-1\right)=0\Leftrightarrow x^5\left(1-x\right)-3x^2\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow-x^5\left(x-1\right)-3x^2\left(x+1\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left[-x^5-3x^3-3x^2\ne0\right]=0\Leftrightarrow x=1\)