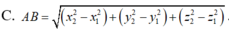K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
23 tháng 10 2019
+ Đạo hàm : y’ = 4/3.x3-28/3. x
y 2 - y 1 = 8 ( x 2 - x 1 ) ⇔ y 2 - y 1 x 2 - x 1 = 8
Vậy tiếp tuyến của (C) tại A có hệ số góc bằng 8.
+ Xét phương trình y' = 8
⇔ 4 3 x 3 - 28 3 x = 8 ⇔ 4 x 3 - 28 x - 24 = 0
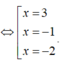
+) Với x= 3 thì A( 3; -15) nên phương trình tiếp tuyến của (C) tại A là y = 8(x-3) - 15 ( d 1 )
Phương trình hoành độ giao điểm của (C) và ( d 1 ) là
8 ( x - 3 ) - 15 = 1 3 x 4 - 14 3 x 2 ⇔ ( x - 3 ) 2 ( x 2 + 6 x + 13 ) = 0 ⇔ x = 3 .
Vậy A(3; -15) loại.
+) Với x= -2 thì A(-2; -40/3) . phương trình tiếp tuyến của (C) tại A là y = 8(x+2) - 40/3 ( d 2 )
Phương trình hoành độ giao điểm của ( C) và ( d 2 ) là
8 ( x + 2 ) - 40 3 = 1 3 x 4 - 14 3 x 2 ⇔ ( x + 2 ) 2 ( x 2 - 4 x - 2 ) = 0
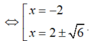
Vậy A( -2; -40/3) thỏa mãn.
+) Với x= -1 thì A( -2; -13/ 3) nên phương trình tiếp tuyến của C tại A là
y = 8(x+1) - 13/3 (d3)
Phương trình hoành độ giao điểm của C và (d3) là:
8 ( x + 1 ) - 13 3 = 1 3 x 4 - 14 3 x 2 ⇔ ( x + 2 ) 2 ( x 2 - 2 x - 11 ) = 0
Vậy A( -1; -13/3) thỏa mãn.
Vậy có tất cả 2 điểm A thỏa mãn yêu cầu bài toán.
Chọn B.
.
.
.
Q
13 tháng 4 2017
Giả sử SABCDS1 là khối 88 mặt đều.
a) Nhận xét rằng:
BA = BC ⇒ B thuộc mặt phẳng trung trực của AC.
DA = DC ⇒ D thuộc mặt phẳng trung trực của AC.
SA = SC ⇒ S thuộc mặt phẳng trung trực của AC.
S1A=S1C ⇒ B thuộc mặt phẳng trung trực của AC.
Từ đó suy ra B, D, S, S1 đồng phẳng và tứ giác SBS1D là hình thoi nên SS1 và BD cắt nhau tại trung điểm mỗi đường (giả sử O).
Chứng minh tương tự, ta có: AC và BD cắt nhau tại trung điểm mỗi đường.
Vậy, ba đường chép của khối 88 mặt đều cắt nhau tại trung điểm của mỗi đường (đpcm)
b) Từ kết quả câu a), vì SBS1D và ABCD là hình thoi nên các đường chéo vuông góc với nhau (đpcm)
c) Ta có:
ΔSAC = ΔBAC (c - c - c) ⇒ SO = BO (1)
ΔSBD = ΔABD (c - c - c) ⇒ SO = AO (2)
Từ đó suy ra AC = BD = SS1(đpcm).
13 tháng 4 2017
Câu c Cm theo cách này đc k?#
Vì EO \(\perp\) (ABCD)
nên OA ; OB lần lượt là hình chiếu của EA; EB trên (ABCD)
mà EA = EB => OA = OB => AC = BD (1)
Cm tương tự: AC = EF (2)
Từ (1),(2) => AC = BD = EF
CM
29 tháng 1 2019
Chọn C.
Gọi 
Khi đó phương trình tiếp tuyến
M
0
là
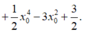
Ta có: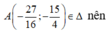 
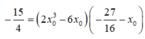
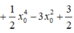
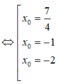
Không mất tính tổng quát của M 1 ( x 1 ; y 1 ) , M 2 ( x 2 ; y 2 ) , M 3 ( x 3 ; y 3 ) , ta có:
