Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
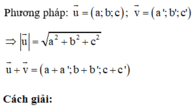
![]()
![]()
=> Đáp án A sai
+) a → + b + c → = 0 => Đáp án D đúng

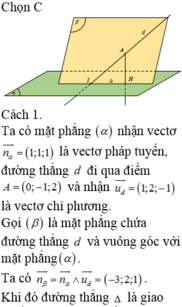
Chọn C
Ta có mặt phẳng α nhận vectơ n α → = ( 1 ; 1 ; 1 ) là vectơ pháp tuyến, đường thẳng d đi qua điểm A(0;-1;2) và nhận u d → = ( 1 ; 2 ; - 1 ) là vectơ chỉ phương.
Gọi β là mặt phẳng chứa đường thẳng d và vuông góc với mặt phẳng α
![]()
Khi đó đường thẳng ∆ là giao tuyến của hai mặt phẳng α và β . Do đó một vectơ chỉ phương của đường thẳng ∆ là .
![]()
Mà u → = ( 1 ; a ; b ) nên a=4, b = -5 => a+b = 4-5 =-1.

Mặt cầu (S) có tâm I(2;-1;2), mặt phẳng (P) có VTPT\(\overrightarrow{n}\)=(1;-1;2). Gọi điểm C(x;y;z) ta có C∈ (S) nên \(\left(x-2\right)^2+\left(y-1\right)^2+\left(z-2\right)^2=4\left(1\right)\)
Do CD là đường kính của mặt cầu (S) nên I là trung điểm của CD
=> D(4-x; -y -2; 4-z)
Mà theo đề có CD//(P) nên
\(\overrightarrow{IC}\perp\overrightarrow{n}\Leftrightarrow\overrightarrow{IC}.\overrightarrow{n}=0\) <=> \(x-2-\left(y+1\right)+2\left(z-2\right)=0\left(2\right)\)
Ta có: \(\overrightarrow{AB}=\left(1;-1;-1\right);\overrightarrow{AC}=\left(x;y-1;z-1\right);\overrightarrow{AD}=\left(4-x;y-3;3-z\right)\)
\(\left|\overrightarrow{AC;}\overrightarrow{AD}\right|=\left(2y+4z-6;-2x+4z-4;-4x-y+4\right)\)
\(\overrightarrow{AB}\left|\overrightarrow{AC};\overrightarrow{AD}\right|=2x+4z-6+\left(-1\right)\left(-2x+4z-4\right)+\left(-1\right)\left(-4x-4y+4\right)=6x+6y-6\)
Thể tích khối tứ diện ABCD là:
V = \(\dfrac{1}{6}\left|\overrightarrow{AB}\left[\overrightarrow{AC};\overrightarrow{AD}\right]\right|=\left|x+y-1\right|\)
Đặt : \(\left\{{}\begin{matrix}x-2=a\\y+1=b\\z-2=c\end{matrix}\right.\)
Từ (1) và (2) có hệ : \(\left\{{}\begin{matrix}a^2+b^2+c^2=4\\a-b+2c=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a-b=-2c\\ab=\dfrac{4-5c^2}{2}\end{matrix}\right.\)
V=|x+y-1| = |x-2+y +1| = |a+b| = \(\sqrt{\left(a-b\right)^2+4ab}\) = \(\sqrt{4c^2+2\left(4-5c^2\right)}=\sqrt{8-6c^2}\le2\sqrt{2}\)
Vậy GTLN của V là 2\(\sqrt{2}\) khi
\(\left\{{}\begin{matrix}z-2=0\\x-2=0\\\left(x-2\right)^2+\left(y-1\right)^2+\left(z-2\right)^2=4\end{matrix}\right.\) <=>\(\left\{{}\begin{matrix}x=2+\sqrt{2};y=-1+\sqrt{2};z=2\\x=2-\sqrt{2};y=-1-\sqrt{2};z=2\end{matrix}\right.\)
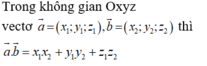
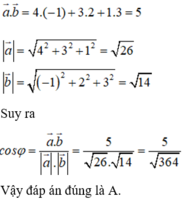



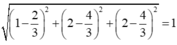
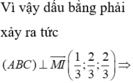
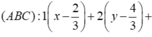
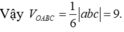
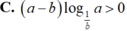
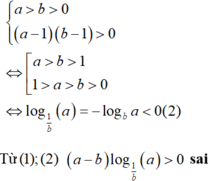
Đáp án C