K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
T
0
AH
Akai Haruma
Giáo viên
24 tháng 11 2021
Lời giải:
Theo định lý Fermat nhỏ thì: $3^{10}\equiv 1\pmod {11}; 4^{10}\equiv 1\pmod {11}$
$\Rightarrow$:
$3^{2021}=(3^{10})^{202}.3\equiv 3\pmod {11}$
$4^{2021}=(4^{10})^{202}.4\equiv 4\pmod {11}$
$\Rightarrow A=3^{2021}+4^{2021}\equiv 3+4\equiv 7\pmod {11}$
Tức $A$ chia $11$ dư $7$
---------------------------------
Tương tự:
$3^{12}\equiv 1\pmod {13}$
$\Rightarrow 3^{2021}=(3^{12})^{168}.3^5\equiv 3^5\equiv 9\pmod {13}$
Tương tự: $4^{2021}\equiv 4^5\equiv 10\pmod {13}$
$\Rightarrow A\equiv 9+10\equiv 6\pmod {13}$
Vậy $A$ chia $13$ dư $6$
28 tháng 9 2016
Giải:
Vì số dư lớn nhất bé hơn số chia 1 đơn vị nên suy ra số dư trong phép chia trên là 24
Số bị chia là:
\(25.23+24=599\)
Vậy số bị chia là 599
HL
0
. Chia 
cho 
được phần dư bằng 2019, chia 
cho 
được phần dư bằng 2018. Gọi 
là phần dư khi chia 
cho 
. Giá trị của 
là
6 tháng 8 2021
Ta có số có 2018 chữ số lớn nhất là 999....99 (2018 chữ số 9)
=> A lỡn nhất là 2018 x 9 = 18162
=> B lớn nhất là 1 + 8 + 1 + 6 + 2 = 18
=> C lớn nhất là 1 + 8 = 9
Ta có 3 x 9 + 2 = 29 mà 29 là số nguyên tố nên không tồn tại số như vậy
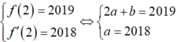
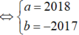
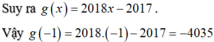
\(\hept{\begin{cases}x:17\left(dư9\right)\\x:19\left(dư13\right)\end{cases}}\Rightarrow\hept{\begin{cases}17-9:x\\19-13:x\end{cases}\Rightarrow\hept{\begin{cases}12⋮x\\6⋮x\end{cases}}\Rightarrow x\inƯC\left(12;6\right)}\)
\(12=2^2.3\)
\(6=2.3\)
\(ƯCLN\left(12;6\right)=2.3=6\)
Vì x<500
nên x={6;12;18;24....;485;490;490}
cho mk xl , số cuối 495 nha !