Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Leftrightarrow\left\{{}\begin{matrix}m^2-1=0\\m^2-2m-3\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\pm1\\m\ne-1;m\ne3\end{matrix}\right.\Leftrightarrow m=1\)
Chọn A

Chọn A.
Bất phương trình ( m 2 + m + 1)x - 5m ≥ ( m 2 + 2)x - 3m - 1 ⇔ (m - 1)x ≥ 2m - 1 vô nghiệm khi
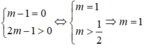

Chọn B.
Xét bất phương trình:
m 2 x + m - 1 < x ⇔ m 2 x - x + m - 1 < 0 ⇔ ( m 2 - 1)x < 1 - m (1)
Với m = 1, bất phương trình (1) trở thành: 0x < 0 ⇔ 0 < 0 (Vô lý) ⇒ Bất phương trình vô nghiệm.
Với m = -1 , bất phương trình (1) trở thành: 0x < 2 ⇔ 0 < 2 (luôn đúng) ⇒ Bất phương trình có vô số nghiệm.
Vậy bất phương trình m 2 x + m - 1 < x vô nghiệm khi m = 1.


Chọn A.
Bất phương trình ( m 2 + m + 1)x - 5m ≥ ( m 2 + 2)x - 3m - 1 ⇔ (m - 1)x ≥ 2m - 1 vô nghiệm khi
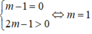

Phương trình có nghiệm kép khi m ≠ -2 và Δ = 0.
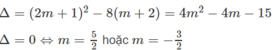
Khi m = 5/2 nghiệm kép của phương trình là
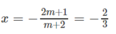
Khi m = -3/2 nghiệm kép của phương trình là x = 2.

a: Ta có: \(\left(m-1\right)x^2-2x-m+1=0\)
a=m-1; b=-2; c=-m+1
\(ac=\left(m-1\right)\left(-m+1\right)=-\left(m-1\right)^2< 0\forall m\)
Do đó: Phương trình luôn có hai nghiệm trái dấu
b: \(x_1^2+x_2^2=6\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=6\)
\(\Leftrightarrow\left(\dfrac{2}{m-1}\right)^2-2\cdot\dfrac{-m+1}{m-1}=6\)
\(\Leftrightarrow\dfrac{4}{\left(m-1\right)^2}=4\)
\(\Leftrightarrow\left(m-1\right)^2=1\)
=>m-1=1 hoặc m-1=-1
=>m=2 hoặc m=0

=>m-1=0
hay m=1
đúng lúc đang thi