
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo BĐT Cô si ta có:
\(4a+\frac{1}{a}\ge2\sqrt{4a\cdot\frac{1}{a}}=4\)
Dấu "=" xảy ra tại \(a=\frac{1}{2}\)
Ta có: \(\left(2a-1\right)^2\ge0\forall a\)
\(\Leftrightarrow4a^2-4a+1\ge0\forall a\)
\(\Leftrightarrow4a^2+1\ge4a\forall a\)
\(\Leftrightarrow\frac{4a^2+1}{a}\ge4\forall a>0\)
\(\Leftrightarrow4a+\frac{1}{a}\ge4\)(đpcm)
Dấu "="\(\Leftrightarrow a=\frac{1}{2}\)

Rút gọn biểu thức ta có :
\(\left(a-\frac{x^2+a^2}{x+a}\right).\left(\frac{2a}{x}-\frac{4a}{x-a}\right)\)
\(=\frac{a\left(x+a\right)-\left(x^2+a^2\right)}{x+}.\frac{2a\left(x-a\right)-4a.x}{x\left(x-a\right)}\)
\(=\frac{ax+a^2-x^2-a^2}{x+a}.\frac{2ax-2a^2-4ax}{x\left(x-a\right)}\)
\(=\frac{ax-x^2}{x+a}.\frac{-2a^2-2ax}{x\left(x-a\right)}\)
\(=\frac{-\left(x^2-ax\right)}{\left(x+a\right)}.\frac{-\left(2a^2+2ax\right)}{x\left(x-a\right)}\)
\(=\frac{\left(x^2-ax\right).\left(2a^2+2ax\right)}{x\left(x+a\right)\left(x-a\right)}\)
\(=\frac{x\left(x-a\right).2a\left(a+x\right)}{x\left(x+a\right)\left(x-a\right)}\)
\(=2a\)
Với a là một số nguyên thì giá trị biểu thức bằng 2a là một số chẵn.
Chúc bạn học tốt !!!

a4 + a3 + a + 1 ≥ 0
<=> a3( a + 1 ) + ( a + 1 ) ≥ 0
<=> ( a + 1 )( a3 + 1 ) ≥ 0
<=> ( a + 1 )2( a2 - a + 1 ) ≥ 0 ( đúng )
Vậy ta có đpcm. Dấu "=" xảy ra <=> a = -1
Ta có: \(a^4+a^3+a+1\)
\(=a^3\left(a+1\right)+\left(a+1\right)\)
\(=\left(a+1\right)\left(a^3+1\right)\)
\(=\left(a+1\right)\left(a+1\right)\left(a^2-a+1\right)\)
\(=\left(a+1\right)^2\left[\left(a^2-a+\frac{1}{4}\right)+\frac{3}{4}\right]\)
\(=\left(a+1\right)^2\left[\left(a-\frac{1}{2}\right)^2+\frac{3}{4}\right]\ge0\left(\forall a\right)\) (luôn đúng)
Dấu "=" xảy ra khi: a = -1

\(=\dfrac{ax-a^2-x^2-a^2}{x+a}\cdot\dfrac{2a\left(x-a\right)-4ax}{x\left(x-a\right)}\)
\(=\dfrac{x\left(a-x\right)}{x+a}\cdot\dfrac{2a\left(x-a-2x\right)}{x\left(x-a\right)}\)
\(=-2a⋮2\)

Bài 1 bạn tham khảo tại đây nhé:
Tim x,y,z thoa man : x^2 +5y^2 -4xy +10x-22y +Ix+y+zI +26 = 0 ...
Chúc bạn học tốt!


Trả lời
a^2 + b^2 - 2ab
= ( a^2 - 2ab + b^2 )
= ( a - b )^2 ≥ 0 ( luôn đúng )
Vậy...

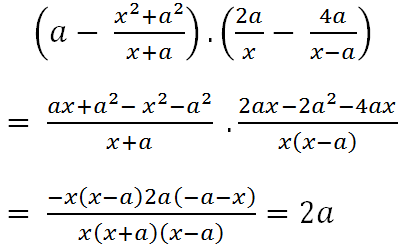 ~~~Học Tốt~~~
~~~Học Tốt~~~
\(4a+\frac{1}{a}\ge4\)
\(\Leftrightarrow4a^2+1\ge4a\)
\(\Leftrightarrow4a^2-4a+1\ge0\)
\(\Leftrightarrow\left(2a\right)^2-2\times2a\times1+1^2\ge0\)
\(\Leftrightarrow\left(2a-1\right)^2\ge0\) đúng
Dấu = xảy ra khi \(a=\frac{1}{2}\)