Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số đối của phân số \(\dfrac{a}{b}\) là \(\dfrac{-a}{b}\) hoặc \(\dfrac{a}{-b}\) hoặc \(-\dfrac{a}{b}\)
Số nghịch đảo của phân số \(\dfrac{a}{b}\) là \(\dfrac{b}{a}\)
Số đối của \(\dfrac{a}{b}\) là \(\dfrac{-a}{b}\) hoặc \(\dfrac{a}{-b}\) hoặc \(-\dfrac{a}{b}\).
Số nghịch đảo của \(\dfrac{a}{b}\) là \(\dfrac{b}{a}\) hoặc \(\dfrac{-b}{-a}\).

Số nghịch đảo của phân số \(\dfrac{a}{b}\)là phân số \(\dfrac{b}{a}\) ; (a ,b ∈ Z , a ≠ 0 , b ≠ 0)

- Số nghịch đảo của 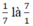
- Số nghịch đảo của 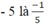
- Số nghịch đảo của 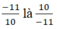
- Số nghịch đảo của

Câu 1:
Số đối của a/b là -a/b
\(\dfrac{a}{b}-\dfrac{c}{d}=\dfrac{ad-bc}{bd}\)
\(\dfrac{a}{b}\cdot\dfrac{c}{d}=\dfrac{ac}{bd}\)
Câu 2:
Số nghịch đảo của a/b là b/a
\(\dfrac{a}{b}:\dfrac{c}{d}=\dfrac{a}{b}\cdot\dfrac{d}{c}=\dfrac{ad}{bc}\)

5.Phân số tối giản là phân số không thể rút gọn được nữa. VD : 4/5
4. muốn rút gọn phân số ta lấy cả tử vs mẫu chia cho 1 số nào đó
VD: \(\frac{10}{15}=\frac{10:5}{15:5}=\frac{2}{3}\)

\(a,\)Số cần tìm là :
\(1:\frac{41}{20}=\frac{20}{41}\)
Vậy.................
b,Ta có :abcd \(⋮9\)và a+b+c+d chia hết cho 9
\(\Rightarrow1000a+100b+10c+d⋮9\)
\(\Rightarrow999a+99b+9c+d+a+b+c⋮9\)
\(=9\left(111a+11b+c\right)+a+b+c+d⋮9\)

VD tổng nghịch đâỏ cảu ba số này là 2 thì:
Số lớn nhất là a, số nhỏ nhất là c.
Ta có: c ≤ b ≤ a (1)
Theo giả thiết : \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) = 2 (2)
Do (1) nên 2 = \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) ≤ \(\dfrac{3}{c}\)
Vậy c = 1
Thay vào (2) ta dc :\(\dfrac{1}{a}+\dfrac{1}{b}\) = 1 ≤ \(\dfrac{2}{b}\)
Vậy a = 2 từ đó b = 2
3 số cần tìm là 1; 2; 2.
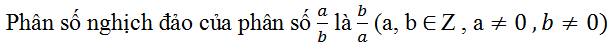
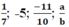
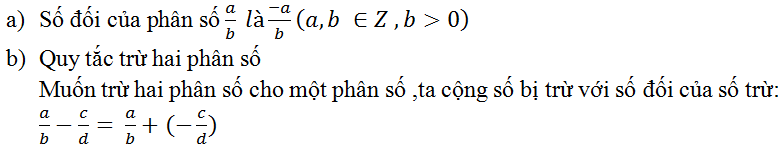
Phân số nghịch đảo của phân số a b là b a a , b ∈ Z , a ≠ 0 , b ≠ 0