Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì (d')//(d) nên a=-1
Vậy: (d'): y=-x+b
Thay x=0 và y=3 vào (d'), ta được: b=3
Gọi \(\left(d'\right):y=ax+b\left(a\ne0\right)\) là đt cần tìm
\(\left(d'\right)\text{//}\left(d\right)\Leftrightarrow a=-1;b\ne1\Leftrightarrow\left(d'\right):y=-x+b\\ A\left(0;3\right)\in\left(d'\right)\Leftrightarrow b=3\)
Vậy \(\left(d'\right):y=-x+3\)

Ta có \(\left(d\right):y=ax+b\) song song với \(\left(d\right):y=3x-1\)
\(\Rightarrow a=3\) ta được phương trình \(y=3x+b\)
đường thẳng này cắt trục tung tại tung độ bằng 2
\(\Rightarrow\left(0;2\right)\)
\(\Rightarrow2=3.0+b\\ \Rightarrow b=2\)

\(a,PTHDGD:2x-1=-x+2\Leftrightarrow x=1\Leftrightarrow y=1\Leftrightarrow M\left(1;1\right)\\ b,\text{Gọi đt của }\left(d\right)\text{ là }y=ax+b\left(a\ne0\right)\\ \Leftrightarrow\left\{{}\begin{matrix}a+b=1\\0a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=4\end{matrix}\right.\Leftrightarrow\left(d\right):y=-3x+4\)

a) Gọi phương trình đường thẳng cần lập là \(y=ax+b\left(d_1\right)\).
Để \(\left(d_1\right)\)//\(\left(d\right)\) thì \(a=2\) \(\Rightarrow\left(d_1\right):y=2x+b\).
Xét phương trình hoành độ giao điểm của \(\left(d_1\right)\) và \(\left(d'\right)\):
\(2x+b=3x-2\Leftrightarrow x=b+2\).
Hai đường thẳng này cắt nhau tại điểm có hoành độ là 2
\(\Leftrightarrow b+2=2\Leftrightarrow b=0\).
Vậy phương trình đường thẳng cần lập là \(\left(d_1\right):y=2x\).
b) Gọi phương trình đường thẳng cần lập là \(y=ax+b\left(d_2\right)\).
\(\left(d_2\right)\perp\left(d'\right)\Leftrightarrow3a=-1\Leftrightarrow a=-\dfrac{1}{3}\)
\(\Rightarrow\left(d_2\right):y=-\dfrac{1}{3}x+b\).
Xét phương trình hoành độ giao điểm của \(\left(d_2\right)\) và \(\left(d\right)\):
\(2x-3=-\dfrac{1}{3}x+b\Leftrightarrow\dfrac{7}{3}x=b+3\Leftrightarrow x=\dfrac{3b+9}{7}\)
\(\Rightarrow y=2x-3=\dfrac{6b-3}{7}\).
Hai đường thẳng này cắt nhau tại điểm có tung độ bằng -1
\(\Leftrightarrow\dfrac{6b-3}{7}=-1\Leftrightarrow6b-3=-7\Leftrightarrow b=-\dfrac{2}{3}\).
Vậy phương trình đường thẳng cần lập là \(\left(d_2\right):y=-\dfrac{1}{3}x-\dfrac{2}{3}\).

Gọi (d): y=ax+b(a<>0) là phương trình đường thẳng cần tìm
Vì (d)//y=-9x+4 nên \(\left\{{}\begin{matrix}a=-9\\b< >4\end{matrix}\right.\)
Vậy: (d): y=-9x+b
Thay y=5 vào y=-3x+2, ta được:
-3x+2=5
=>-3x=3
=>\(x=\dfrac{3}{-3}=-1\)
Thay x=-1 và y=5 vào y=-9x+b, ta được:
\(b-9\cdot\left(-1\right)=5\)
=>b+9=5
=>b=-4
Vậy: (d): y=-9x-4 là phương trình đường thẳng cần tìm

Đề không rõ ràng. Bạn coi lại đề. Những dữ kiện trên được chia theo phần hay là cả 1 cụm?
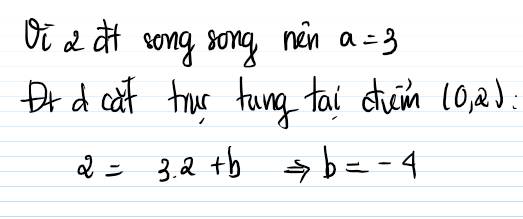
Vì (d)//(d') nên a=3
Vậy: y=3x+b
Thay x=0 và y=4 vào y=3x+b, ta được:
b=4