Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

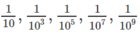
Dự đoán dãy (un) giảm.
Để chứng minh, ta xét tỉ số
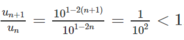 .
.
Vậy dãy số giảm

a)
\(u_1=10^{1-2.1}=10^{-1};u_2=10^{1-2.2}=10^{-3}\);
\(u_3=10^{1-2.3}=10^{-5}\); \(u_4=10^{1-2.4}=10^{-7}\);
\(u_5=10^{1-2.5}=10^{-9}\).
Xét \(\dfrac{u_n}{u_{n-1}}=\dfrac{10^{1-2n}}{10^{1-2\left(n-1\right)}}=\dfrac{10^{1-2n}}{10^{3-2n}}=10^{-2}=\dfrac{1}{100}\).
Suy ra: \(u_n=\dfrac{1}{100}u_{n-1}\) và dễ thấy \(\left(u_n\right)>0,\forall n\in N^{\circledast}\) nên \(u_n< u_{n-1},\forall n\ge2\).
Vậy \(\left(u_n\right)\) là dãy số tăng.
b) \(u_1=3^1-7=-4\); \(u_2=3^2-7=2\); \(u_3=3^3-7=25\);
\(u_4=3^4-7=74\); \(u_5=3^5-7=236\).
\(u_n-u_{n-1}=3^n-7-\left(3^{n-1}-7\right)=3^n-3^{n-1}=2.3^{n-1}\)\(\left(n\ge2\right)\).
Với \(n\ge2\) thì \(2.3^{n-1}>0\) nên \(u_n>u_{n-1}\).
Vậy \(\left(u_n\right)\) là dãy số tăng.

a) Vì hàm số \(u\) xác định trên tập hợp các số nguyên dương
\(\mathbb{N}^{\text{∗
}}\) nên nó là một dãy số vô hạn.
b) Ta có:
\(u_1=1^3=1\\ u_2=2^3=8\\ u_3=3^3=27\\ u_4=4^3=64\\ u_5=5^3=125.\)

a) Ta có: \({u_{n + 1}} = \frac{{{{\left( {n + 1} \right)}^2}}}{{n + 1 + 1}} = \frac{{{{\left( {n + 1} \right)}^2}}}{{n + 2}}\)
Xét hiệu \({u_{n + 1}} - {u_n} = \frac{{{{\left( {n + 1} \right)}^2}}}{{n + 2}} - \frac{{{n^2}}}{{n + 1}} = \frac{{{{\left( {n + 1} \right)}^3} - {n^2}\left( {n + 2} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}} = \frac{{{n^3} + 3{n^2} + 3n + 1 - {n^3} - 2{n^2}}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\)
\( = \frac{{{n^2} + 3n + 1}}{{\left( {n + 2} \right)\left( {n + 1} \right)}} > 0\) với mọi n ∈ ℕ*.
Vì vậy dãy số đã cho là dãy số tăng.
b) Ta có: \({u_{n + 1}} = \frac{2}{{{5^{n + 1}}}}\)
Xét hiệu \({u_{n + 1}} - {u_n} = \frac{2}{{{5^{n + 1}}}} - \frac{2}{{{5^n}}} = - \frac{4}{5}.\frac{2}{{{5^n}}} = - \frac{8}{{{5^{n + 1}}}} < 0\)
Vì vậy dãy số đã cho là dãy số giảm.
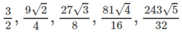
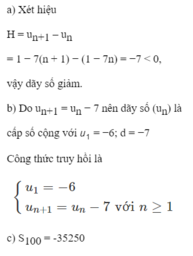
Xét dấu của hiệu u n + 1 - u n