PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
PT
1
PT
1
PT
1
CM
6 tháng 9 2017
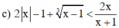
BPT xác định khi x + 1 ≠ 0 ⇔ x ≠ –1.
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{–1}
CM
16 tháng 2 2018
Điều kiện của (1) và điều kiện của (2) là
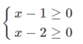
Hai bất phương trình đã cho không tương đương với nhau vì có x = -1 là một nghiệm của (1) nhưng không là nghiệm của (2).
Nhận xét:Phép biến đổi đồng nhất 
làm mở rộng tập xác định, dẫn tới thay đổi điều kiện của phương trình, do đó có thể làm xuất hiện nghiệm ngoại lai.
PT
1
CM
7 tháng 2 2018
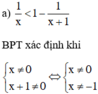
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{0; –1}
BT
8 tháng 5 2017
Bất phương trình (1) :
Đkxđ: \(\left(x-1\right)\left(x-2\right)\ge0\)\(\Leftrightarrow\left[{}\begin{matrix}x\ge2\\x\le1\end{matrix}\right.\)
Bất phương trình (2):
Đkxđ: \(\left\{{}\begin{matrix}x-1\ge0\\x-2\ge0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\x\ge2\end{matrix}\right.\)\(\Leftrightarrow x\ge2\).
Vậy hai bất phương trình không tương đương.
NT
2
CM
21 tháng 9 2018
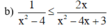
BPT xác định khi
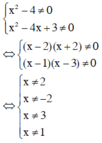
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{–2; 1; 2; 3}
Điều kiện là x tùy ý.