Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

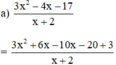
(Tách -4x = 6x – 10x để nhóm với 3x2 xuất hiện x + 2)
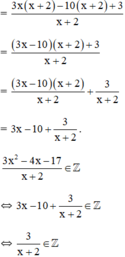
⇔ x + 2 ∈ Ư(3) = {±1; ±3}
+ x + 2 = 1 ⇔ x = -1
+ x + 2 = -1 ⇔ x = -3
+ x + 2 = 3 ⇔ x = 1
+ x + 2 = -3 ⇔ x = -5
Vậy với x = ±1 ; x = -3 hoặc x = -5 thì phân thức có giá trị nguyên.
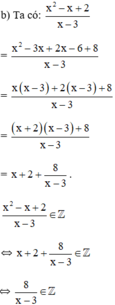
⇔ x – 3 ∈ Ư(8) = {±1; ±2; ±4; ±8}
+ x – 3 = 1 ⇔ x = 4
+ x – 3 = -1 ⇔ x = 2
+ x – 3 = 2 ⇔ x = 5
+ x – 3 = -2 ⇔ x = 1
+ x – 3 = 4 ⇔ x = 7
+ x – 3 = -4 ⇔ x = -1
+ x – 3 = 8 ⇔ x = 11
+ x – 3 = -8 ⇔ x = -5.
Vậy với x ∈ {-5; -1; 1; 2; 4; 5; 7; 11} thì giá trị phân thức là số nguyên.

a, \(\frac{2x+1}{2x^2-5x-3}\)
b, \(\frac{2x+1}{2x^2-5x-3}\)
\(=\frac{2x+1}{2x^2+x-6x-3}\)
\(=\frac{2x+1}{x\left(2x+1\right)-3\left(2x+1\right)}\)
\(=\frac{2x+1}{\left(2x+1\right)\left(x-3\right)}\)
\(=\frac{1}{x-3}\)

Đề bài bạn viết hơi khó hiểu, nhưng có thể tạm giải như sau:
Lời giải:
$A=\frac{4x^2}{x+1}=\frac{4(x^2-1)+4}{x+1}=\frac{4(x-1)(x+1)+4}{x+1}$
$=4(x-1)+\frac{4}{x+1}$
Với $x$ nguyên thì:
$A\in\mathbb{Z}\Leftrightarrow 4(x-1)+\frac{4}{x+1}\in\mathbb{Z}$
$\Leftrightarrow \frac{4}{x+1}\in\mathbb{Z}$
$\Leftrightarrow x+1$ là ước của $4$
$\Rightarrow x+1\in\left\{\pm 1;\pm 2;\pm 4\right\}$
$\Rightarrow x\in\left\{-2; 0; -3; 1; 3; -5\right\}$

a) \(A=\frac{\left(2x\right)^2-\left(2x\right)+7}{\left(2x\right)-1}=\frac{\left(2x\right)\left(2x-1\right)+7}{\left(2x-1\right)}=2x+\frac{7}{\left(2x-1\right)}\)dk x khac 1/2
b) 2x-1=U(7)=> x={-3,0,1,4)