NK
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 9 2023
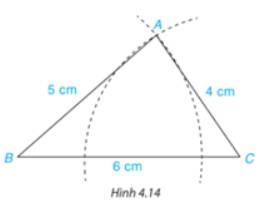
a) Vì 5+4 > 6 nên ba độ dài 5 cm, 4 cm, 6 cm có thể là độ dài ba cạnh của một tam giác.
b) Vì 3 + 6 = 9 < 10 nên ba độ dài 3 cm, 6 cm, 10 cm không thể là độ dài ba cạnh của một tam giác
NT
4
VN
18 tháng 1 2017
Chứng minh tam giác vuông mà thấy số liệu là mừng chết mất =)))
Xét tam giác MNP có:
\(MN^2=NP^2+MP^2\)
\(10^2=6^2+8^2\)
\(100=36+64\)
Vậy trong tam giác này sử dụng được pytago
=> Tam giác MNP vuông tại P
Hình dễ lắm b. Lúc này hình chưa chứng minh là vuông nhé :)
VN
18 tháng 1 2017
Bây giờ mới để ý chỗ đề viết sai. Tam giác MNP chứ lấy đâu ra R? :)
MN
10 tháng 4 2021
AB = KN = 10 (cm)
AC = KP = 5 (cm)
Chu vi tam giác KNP :
10 + 5 + 8 = 23 (cm)
=> D
AM
28 tháng 1 2022
a. Ta có: \(AB^2+AC^2=6^2+8^2=100=BC^2\)
Áp dụng định lí Py-ta-go đảo ta có: tam giác ABC vuông tại A
b. Xét \(\Delta ABD\) vuông tại A và \(\Delta EBD\) vuông tại E có: \(\left\{{}\begin{matrix}BDchung\\\widehat{ABD}=\widehat{EBD}\end{matrix}\right.\)
\(\Rightarrow\)\(\Delta ABD\)=\(\Delta EBD\) \(\Rightarrow\)DA=DE(dpcm)
c. Xét \(\Delta FAD\) vuông tại A và \(\Delta CED\) vuông tại E có: \(\left\{{}\begin{matrix}DA=DE\\\widehat{ADF}=\widehat{EDC}\end{matrix}\right.\)
\(\Rightarrow\)\(\Delta FAD\)=\(\Delta CED\)\(\Rightarrow\)AF=EC
Mà BF=AB+BF, BC=BE+EC, AF=EC, AB=BE
\(\Rightarrow\)BF=BC\(\Rightarrow\)\(\Delta BFC\) cân tại B
d. Xét \(\Delta BFC\) cân tại B có: CA,FE là đường cao giao nhau tại D
\(\Rightarrow\)BD cũng là đường cao của \(\Delta BFC\)
mà \(\Delta BFC\) cân tại B nên BD vừa là đường cao vừa là đường trung tuyến
\(\Rightarrow\) BD là đường trung trực (dpcm)
19 tháng 6 2023
a: Trực tâm là điểm D
b: EF=căn 3^2+4^2=5cm
c: DF=căn 10^2-6^2=8cm
tự đánh điểm
bước 1: vẽ đoạn thẳng ZU =10 cm
bước 2 : dùng khẩu độ compa 5cm để vẽ cung trón tâm U
bước 3: dùng khẩu độ compa 6 cm để vẽ cung tròn tâm Z
bước 4: hai cung tròn cắt nhau ở V
bước 5: nối các đỉnh với nhau ta được tam giác UVZ