K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DT
24 tháng 5 2022
thm khao :
https://hoc247.net/toan-11/bai-6-on-tap-chuong-3-vecto-trong-khong-gian-quan-he-vuong-goc-trong-khong-gian-l6419.html
MM
0
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
Ta dùng sơ đồ hình cây để mô tả như sau:
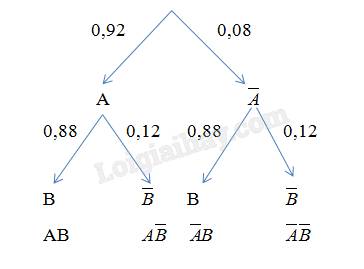
Theo sơ đồ hình cây, ta có:
a) \(P\left( {A\overline B } \right) = 0,92.0,12 = 0,1104\)
b) \(P\left( {\overline A B} \right) = 0,08.0,88 = 0,0704\)
c) \(P\left( {\overline A \overline B } \right) = 0,08.0,12 = 0,0096\)
\(P\left( {A \cup B} \right) = 1 - P\left( {\overline A \overline B } \right) = 1 - 0,0096 = 0,9904\)
ML
26 tháng 7 2023
Hiện tại sách là chương trình mới những vẫn không có PowerPoint bạn nha. Nên hiện tại chưa biết được khi nào sẽ có PowerPoint, nhưng ở các lớp dưới thì cũng đã học rồi á bạn.
KV
27 tháng 7 2023
Theo chương trình sgk mới thì lớp 7, lớp 8 có học PowerPoint. Lớp 11 thì chưa có em nhé!
CM
11 tháng 4 2017
Chọn D
Nhóm có tất cả 9 học sinh nên số cách xếp 9 học sinh này ngồi vào một hàng có 9 ghế là 9! = 362880(cách).
Vậy số phần tử không gian mẫu là n ( Ω ) = 362880
Đặt biến cố A: “ 3 học sinh lớp không ngồi ghế liền nhau”.
Giả sử học sinh lớp 10 ngồi 3 ghế liền nhau. Ta xem 3 học sinh này là một nhóm
+/ Xếp X và 6 bạn còn lại vào ghế có 7! cách xếp.
+/ Ứng với mỗi cách xếp ở trên, có 3! cách xếp các bạn trong nhóm X.
Vậy theo quy tắc nhân ta có số cách xếp là: 7!.3! = 30240 (cách).
Suy ra số cách xếp để học sinh lớp không ngồi cạnh nhau là (cách) .
Vậy xác suất để học sinh lớp 10 không ngồi cạnh nhau là 362880 - 30240 = 332640 (cách)
=> n(A) = 332640
Vậy xác suất để học sinh lớp 10 không ngồi cạnh nhau là
CM
15 tháng 6 2018
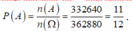
Do mỗi học sinh lớp 12 ngồi giữa hai học sinh khối 11 nên ở vị trí đầu tiên và cuối cùng của dãy ghế sẽ là học sinh khối 11.
Bước 1: Xếp 6 học sinh lớp 11 thành một hàng ngang, có 6! cách.
Bước 2: giữa 6 bạn học sinh lớp 11 có 5 khoảng trống, chọn 3 khoảng trống trong 5 khoảng trống để xếp các bạn lớp 12, có 
cách( có liên quan đến thứ tự).
Theo quy tắc nhân có 
cách xếp thỏa yêu cầu.
Chọn C.
CM
19 tháng 1 2017
Chọn 3 học sinh lớp 12 có 
cách
Chọn 1 học sinh lớp 11 có 
cách
Chọn 1 học sinh lớp 10 có 
cách.
Do đó có 
cách chọn.
Chọn B.
refer
https://hoc247.net/toan-11/bai-6-on-tap-chuong-3-vecto-trong-khong-gian-quan-he-vuong-goc-trong-khong-gian-l6419.html