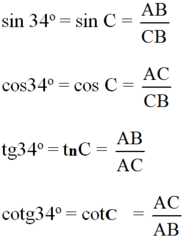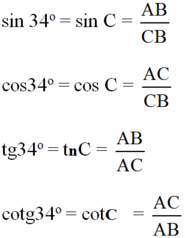NL
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
PT
1
B1
31 tháng 8 2017
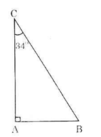
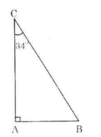
Bài 10. Vẽ một tam giác vuông có một góc nhọn 34∘34∘ rồi viết các tỉ số lượng giác của góc 34∘34∘.
Hướng dẫn giải:
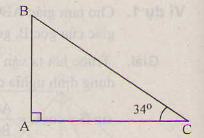
Vẽ tam giác ABC vuông tại A, ˆC=34∘C^=34∘
Theo định nghĩa ta có:
sin34∘=ABBCsin34∘=ABBC
cos34∘=ACBCcos34∘=ACBC
tg34∘=ABACtg34∘=ABAC
cotg34∘=ACABcotg34∘=ACAB.
Xem thêm tại: http://loigiaihay.com/bai-10-trang-76-sgk-toan-9-tap-1-c44a2814.html#ixzz4rLOPb3I0
DP
2
HH
16 tháng 7 2020
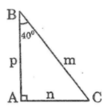
Vẽ tam giác ABC vuông tại A có \(\widehat{B}=90^o\)
Đặt AB = p ; AC = n ; BC = m
Ta có : \(sin40^o=sin\widehat{B}=\frac{AC}{BC}=\frac{n}{m}\)
\(cos40^o=cos\widehat{B}=\frac{AB}{BC}=\frac{p}{m}\)
\(tg40^o=tg \widehat{B } =\frac{AC}{AB}=\frac{n}{p}\)
\(cotg40^o=cotg \widehat{B} =\frac{AB}{AC}=\frac{p}{n}\)
LT
23 tháng 9 2021
Vẽ ∆ góc C = 40°
Góc A = 90°
→ Góc B = 50°
GIẢI
Tỉ số lượng giác của góc 40° là
Sin = AC/BC
Cos = AB/BC
Tg = AC/AB
Cot = AB/AC
SG
3
NL
24 tháng 4 2017
Vẽ tam giác ABC vuông tại A, góc C = 34°
Theo định nghĩa ta có:
24 tháng 4 2017
Hướng dẫn giải:
Vẽ tam giác ABC vuông tại A, ˆC=34∘C^=34∘
Theo định nghĩa ta có:
sin34∘=ABBCsin34∘=ABBC
cos34∘=ACBCcos34∘=ACBC
tg34∘=ABACtg34∘=ABAC
cotg34∘=ACABcotg34∘=ACAB.
7 tháng 9 2021
a: Xét ΔBAC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay BC=5(cm)
b: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=2,4\left(cm\right)\\BH=1,8\left(cm\right)\\CH=3,2\left(cm\right)\end{matrix}\right.\)
17 tháng 10 2021
a: \(\widehat{B}=60^0\)
AB=8cm
\(AC=4\sqrt{3}\left(cm\right)\)